题目内容
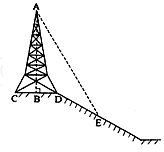
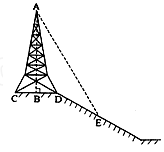
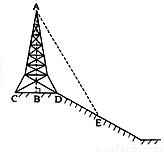
如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,那么塔高AB为 米.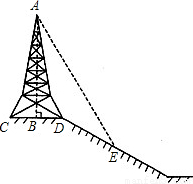
【答案】分析:本题的关键是仔细观察图形,理解铁塔AB的影子是由坡面DE与平地BD两部分组成.
塔影落在坡面部分的塔高:塔影DE长=小明的身高:小明的影长;
塔影落在平地部分的塔高:塔影BD长=小华的身高:小华的影长.
设塔影留在坡面DE部分的塔高为h1、塔影留在平地BD部分的塔高为h2,则铁塔的高为h1+h2.
解答: 解:过D点作DF∥AE,交AB于F点,
解:过D点作DF∥AE,交AB于F点,
设塔影留在坡面DE部分的塔高AF=h1、塔影留在平地BD部分的塔高BF=h2,则铁塔的高为h1+h2.
∵h1:18m=1.6m:2m,∴h1=14.4m;
∵h2:6m=1.6m:1 m,∴h2=9.6m.
∴AB=14.4+9.6=24(m).
∴铁塔的高度为24m.
故答案为:24.
点评:解决本题的难点是把塔高的影长分为在平地和斜坡上两部分;关键是利用平地和斜坡上的物高与影长的比得到相应的部分塔高的长度.
塔影落在坡面部分的塔高:塔影DE长=小明的身高:小明的影长;
塔影落在平地部分的塔高:塔影BD长=小华的身高:小华的影长.
设塔影留在坡面DE部分的塔高为h1、塔影留在平地BD部分的塔高为h2,则铁塔的高为h1+h2.
解答:
 解:过D点作DF∥AE,交AB于F点,
解:过D点作DF∥AE,交AB于F点,设塔影留在坡面DE部分的塔高AF=h1、塔影留在平地BD部分的塔高BF=h2,则铁塔的高为h1+h2.
∵h1:18m=1.6m:2m,∴h1=14.4m;
∵h2:6m=1.6m:1 m,∴h2=9.6m.
∴AB=14.4+9.6=24(m).
∴铁塔的高度为24m.
故答案为:24.
点评:解决本题的难点是把塔高的影长分为在平地和斜坡上两部分;关键是利用平地和斜坡上的物高与影长的比得到相应的部分塔高的长度.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 9、如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,那么塔高AB为
9、如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,那么塔高AB为