题目内容
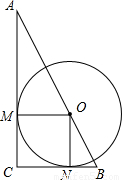
(2005•南充)如图,点O是Rt△ABC斜边上一点,⊙O与AC,BC分别相切于点M,N.(1)△AMO是否相似于△ONB?______(填“是”或“否”);
(2)如果OA=4,OB=3,⊙O的半径为______.
【答案】分析:(1)是.根据切线的性质定理得到直角三角形,再根据等角的余角相等,证明两个直角三角形的一对锐角相等,则两角对应相等,两个三角形相似;
(2)设圆的半径是r,根据相似三角形的对应边的比相等即可求得.
解答:解:(1)∵⊙O与AC,BC分别相切于点M,N,
∴O M⊥AC,ON⊥BC,
在△AMO和△ONB中,∠AMO=∠ONB=90°,
又∵BC⊥AC,OM⊥AC,
∴OM∥BC,
∴∠AOM=∠OBN,
故△AMO∽△ONB;
(2)∵OM∥CN,ON∥CM,OM=ON,∠C是直角,
∴四边形CMON是正方形,
设⊙O的半径为r,即OM=ON=CM=CN=r,
在Rt△AMO中,AM= ,
,
又∵△AMO∽△ONB,
∴ ,
,
故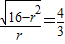 ,
,
解得: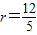 ,
,
即⊙O的半径是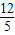 .
.
故应该填是 .
.
点评:熟悉切线的性质定理,掌握相似三角形的判定和性质.
(2)设圆的半径是r,根据相似三角形的对应边的比相等即可求得.
解答:解:(1)∵⊙O与AC,BC分别相切于点M,N,
∴O M⊥AC,ON⊥BC,
在△AMO和△ONB中,∠AMO=∠ONB=90°,
又∵BC⊥AC,OM⊥AC,
∴OM∥BC,
∴∠AOM=∠OBN,
故△AMO∽△ONB;
(2)∵OM∥CN,ON∥CM,OM=ON,∠C是直角,
∴四边形CMON是正方形,
设⊙O的半径为r,即OM=ON=CM=CN=r,
在Rt△AMO中,AM=
 ,
,又∵△AMO∽△ONB,
∴
 ,
,故
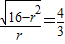 ,
,解得:
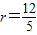 ,
,即⊙O的半径是
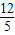 .
.故应该填是
 .
.点评:熟悉切线的性质定理,掌握相似三角形的判定和性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目