题目内容
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.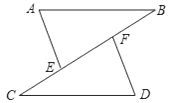
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
【答案】
(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△CDF中,
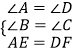 ,
,
∴△ABE≌△CDF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△CDF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFE= ![]() (180°-40°)=70°
(180°-40°)=70°
【解析】(1)由平行线的性质得出∠B=∠C,然后由AAS判断出△ABE≌△CDF,根据三角形全等对应边相等得出结论;
(2)根据全等三角形的性质得出AB=CD,BE=CF,∠B=∠C,,然后根据等边对等角得出∠D=∠CFE,从而得出结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
