题目内容
(2006•福州)对于任意两个二次函数:y1=a1x2+b1x+c1,y2=a2x2+b2x+c2,(a1a2≠0),当|a1|=|a2|时,我们称这两个二次函数的图象为全等抛物线.现有△ABM,A(-1,0),B(1,0).记过三点的二次函数抛物线为“C□□□”(“□□□”中填写相应三个点的字母)
(1)若已知M(0,1),△ABM≌△ABN(0,-1).请通过计算判断CABM与CABN是否为全等抛物线;
(2)在图2中,以A、B、M三点为顶点,画出平行四边形.
①若已知M(0,n),求抛物线CABM的解析式,并直接写出所有过平行四边形中三个顶点且能与CABM全等的抛物线解析式.
②若已知M(m,n),当m,n满足什么条件时,存在抛物线CABM根据以上的探究结果,判断是否存在过平行四边形中三个顶点且能与CABM全等的抛物线?若存在,请列出所有满足条件的抛物线“C□□□”;若不存在,请说明理由.



【答案】分析:(1)应该是全等抛物线,由于这两个抛物线虽然开口方向不同,但是开口大小一样,因此二次项的绝对值也应该相等.可用待定系数法求出两抛物线的解析式,然后进行判断即可.
(2)与(1)相同都是通过构建平行四边形来得出与△ABM全等的三角形,那么过与△ABM全等的三角形的三个顶点的抛物线都是与CABM全等的抛物线.
解答: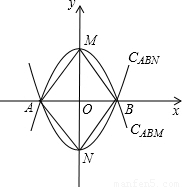 解:(1)设抛物线CABM的解析式为y=ax2+bx+c,
解:(1)设抛物线CABM的解析式为y=ax2+bx+c,
∵抛物线CABM过点A(-1,0),B(1,0),M(0,1),


∴抛物线CABM的解析式为y=-x2+1,
同理可得抛物线CABN的解析式为y=x2+1,
∵|-1|=|1|,
∴CABM与CABN是全等抛物线.
(2)①设抛物线CABM的解析式为y=ax2+bx+c,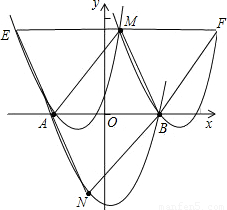
∵抛物线CABM过点A(-1,0),B(1,0),M(0,n),
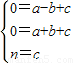
抛物线CABM的解析式为y=-nx2+n,
与CABM全等的抛物线有:
y=nx2-n,y=n(x-1)2,y=n(x+1)2
②当n≠0且m≠±1时,存在抛物线CABM,与CABM全等的抛物线有:CABN,CAME,CBMF.
点评:本题是函数与几何结合的综合题,解题关键是善于利用几何图形的性质以及函数的性质和定理等知识,主要考查学生数形结合的数学思想方法.
(2)与(1)相同都是通过构建平行四边形来得出与△ABM全等的三角形,那么过与△ABM全等的三角形的三个顶点的抛物线都是与CABM全等的抛物线.
解答:
 解:(1)设抛物线CABM的解析式为y=ax2+bx+c,
解:(1)设抛物线CABM的解析式为y=ax2+bx+c,∵抛物线CABM过点A(-1,0),B(1,0),M(0,1),


∴抛物线CABM的解析式为y=-x2+1,
同理可得抛物线CABN的解析式为y=x2+1,
∵|-1|=|1|,
∴CABM与CABN是全等抛物线.
(2)①设抛物线CABM的解析式为y=ax2+bx+c,

∵抛物线CABM过点A(-1,0),B(1,0),M(0,n),
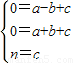
抛物线CABM的解析式为y=-nx2+n,
与CABM全等的抛物线有:
y=nx2-n,y=n(x-1)2,y=n(x+1)2
②当n≠0且m≠±1时,存在抛物线CABM,与CABM全等的抛物线有:CABN,CAME,CBMF.
点评:本题是函数与几何结合的综合题,解题关键是善于利用几何图形的性质以及函数的性质和定理等知识,主要考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
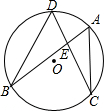 (2006•福州质检)如图,⊙O中弦AB、CD相交于点E,连接BD、AC,则图中相等的角共有( )对.
(2006•福州质检)如图,⊙O中弦AB、CD相交于点E,连接BD、AC,则图中相等的角共有( )对.
 (2006•福州质检)七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,如图是一副七巧板,若已知其中一块平行四边形PHQD的面积是8,请根据你对七巧板制作过程的认识,求动点A沿A→B→E→F→H→P→D所走过的所有路线的长.
(2006•福州质检)七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,如图是一副七巧板,若已知其中一块平行四边形PHQD的面积是8,请根据你对七巧板制作过程的认识,求动点A沿A→B→E→F→H→P→D所走过的所有路线的长.