题目内容
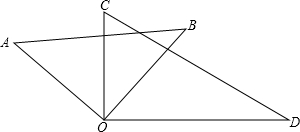 如图,将一幅角板的直角顶点叠放在一起.
如图,将一幅角板的直角顶点叠放在一起.
(1)猜想∠AOC与∠BOD的大小关系,并说明理由;
(2)求∠AOD+∠BOC的度数;
(3)若∠BOD:∠AOD=2:11,求∠BOC的度数.
解:(1)∠AOC=∠BOD,
理由是:∵∠AOB=∠COD=90°,
∴∠AOB-∠COB=∠COD-∠COB,
∴∠AOC=∠BOD;
(2)∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC
=∠AOC+∠BOC+∠BOD+∠BOC
=∠AOB+∠COD
=90°+90°
=180°;
(3)∵∠BOD:∠AOD=2:11,
∴设∠BOD=2a°,∠AOD=11a°,
∵∠AOC=∠BOD,
∴∠BOD=2a°,
∴∠BOC=∠AOD-∠AOC-∠BOD=7a°,
∵由(2)知:∠AOD+∠BOC=180°,
∴11a+7a=180°,
a=10°,
∴∠BOC=70°.
分析:(1)根据∠AOB=∠COD,两边都减去∠COB即可得出答案;
(2)求出∠AOD+∠BOC=∠AOB+∠COD,代入求出即可;
(3)设∠BOD=2a°,∠AOD=11a°,求出∠BOD=2a°,∠BOC=7a°,根据∠AOD+∠BOC=180°得出方程11a+7a=180°,求出即可.
点评:本题考查了角的有关计算,主要考查学生根据图形进行计算的能力,题目比较好,但有一定的难度.
理由是:∵∠AOB=∠COD=90°,
∴∠AOB-∠COB=∠COD-∠COB,
∴∠AOC=∠BOD;
(2)∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC
=∠AOC+∠BOC+∠BOD+∠BOC
=∠AOB+∠COD
=90°+90°
=180°;
(3)∵∠BOD:∠AOD=2:11,
∴设∠BOD=2a°,∠AOD=11a°,
∵∠AOC=∠BOD,
∴∠BOD=2a°,
∴∠BOC=∠AOD-∠AOC-∠BOD=7a°,
∵由(2)知:∠AOD+∠BOC=180°,
∴11a+7a=180°,
a=10°,
∴∠BOC=70°.
分析:(1)根据∠AOB=∠COD,两边都减去∠COB即可得出答案;
(2)求出∠AOD+∠BOC=∠AOB+∠COD,代入求出即可;
(3)设∠BOD=2a°,∠AOD=11a°,求出∠BOD=2a°,∠BOC=7a°,根据∠AOD+∠BOC=180°得出方程11a+7a=180°,求出即可.
点评:本题考查了角的有关计算,主要考查学生根据图形进行计算的能力,题目比较好,但有一定的难度.

练习册系列答案
相关题目
某校团委生活部为了了解本校九年级学生的睡眠情况,随机调查了九年级部分学生的睡眠时间情况,并绘制了如下的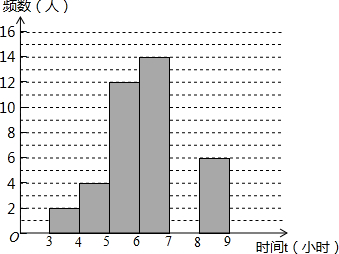 频数分布表和频数分布直方图.
频数分布表和频数分布直方图.
| 组别 | 频数 | 频率 |
| 3~4 | 2 | 0.04 |
| 4~5 | 4 | |
| 5~6 | 12 | |
| 6~7 | 14 | |
| 7~8 | 0.24 | |
| 8~9 | 0.12 | |
| 合计 | 1.00 |
请你根据以上提供的信息,解答下列问题
(1)本次共抽取多少名学生.
(2)补画频数分布直方图;
(3)若初中生合理的睡眠时间范围为7≤t≤9,那么请你估算该校500名九年级学生睡眠时间在此范围内的人数是多少?
 和1-
和1-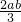
 a2b与-ab2
a2b与-ab2