Question

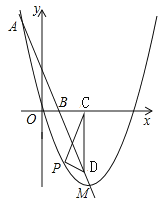
【题目】已知：如图，在平面直角坐标系，直线AB与x轴交于点A(-2，0)，与反比例函数在第一象限内的图象的交于点B(2，n)，连接BO，若=4．

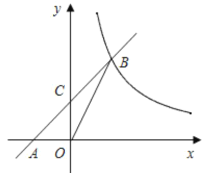
(1)求该反比例函数的解析式和直线AB的解析式；

(2)设直线AB交y轴于点C，点C是否为线段AB的中点？请说明理由．

Answer 1

【答案】（1），；（2）点是线段的中点，理由见解析.

【解析】

（1）先由A（-2，0），得OA=2，点B（2，n），S△AOB=4，得OAn=4，n=4，则点B的坐标是（2，4），把点B（2，4）代入反比例函数的解析式为，可得反比例函数的解析式为：；再把A（-2，0）、B（2，4）代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2．

（2）由（1）中求得的AB的直线解析式求出C点的坐标，再结合A,B的坐标，判断C是否为线段AB的中点.

解：（1）由，得 ．∵点在第一象限内，．

∴．∴．∴点的坐标是．

设该反比例函数的解析式为．将点的坐标代入，得 ，

∴．∴反比例函数的解析式为．

设直线的解析式为．将点，的坐标分别代入，得

解得 ∴直线的解析式为．

（2）点是线段的中点，理由：

∵直线的解析式为，当x=0时，y=2,

∴C（0，2）.

∵，B,

∴=0，=2.

∴C为线段AB的中点.