题目内容
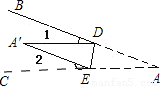
如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,A′E与AE重合,若∠A=30°,则∠1+∠2= .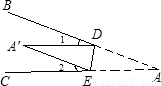
【答案】分析:由折叠的性质,可得:∠A′=∠A=30°,利用三角形的内角和定理与邻补角的性质即可求得∠1+∠2的值.
解答:解:根据题意得:∠A′=∠A=30°,
在△ADE与△A′DE中,∠A+∠ADE+∠AED=180°,∠A′+∠A′DE+∠A′ED=180°,
∴∠ADE+∠AED=150°,∠A′DE+∠A′ED=150°,
∵(∠1+∠A′DE+∠ADE)+(∠AED+∠A′ED+∠2)=180°+180°=360°,
∴∠1+∠2=60°.
故答案为:60°.
点评:此题考查了三角形内角和定理与折叠的性质.解题的关键是数形结合思想的合理应用.
解答:解:根据题意得:∠A′=∠A=30°,
在△ADE与△A′DE中,∠A+∠ADE+∠AED=180°,∠A′+∠A′DE+∠A′ED=180°,
∴∠ADE+∠AED=150°,∠A′DE+∠A′ED=150°,
∵(∠1+∠A′DE+∠ADE)+(∠AED+∠A′ED+∠2)=180°+180°=360°,
∴∠1+∠2=60°.
故答案为:60°.
点评:此题考查了三角形内角和定理与折叠的性质.解题的关键是数形结合思想的合理应用.

练习册系列答案
相关题目
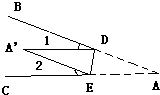 16、如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,A′E与AE重合,若∠A=30°,则∠1+∠2=
16、如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,A′E与AE重合,若∠A=30°,则∠1+∠2=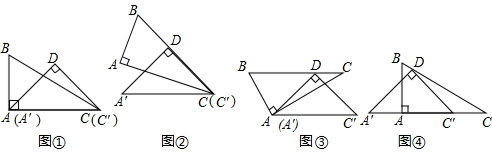
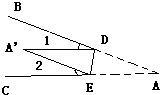 如图,将∠BAC沿DE向∠BAC内折叠,使AD与A’D重合,A’E与AE重合,若∠A=30°,则∠1+∠2=( )
如图,将∠BAC沿DE向∠BAC内折叠,使AD与A’D重合,A’E与AE重合,若∠A=30°,则∠1+∠2=( )