题目内容
 如图已知△ABC内,P、Q分别在BC,CA上,并且AP、BQ分别是∠BAC、∠ABC的平分线.
如图已知△ABC内,P、Q分别在BC,CA上,并且AP、BQ分别是∠BAC、∠ABC的平分线.(1)若∠BAC=60°,∠ACB=40°,求证:BQ+AQ=AB+BP;
(2)若∠ACB=α时,其他条件不变,直接写出∠BAC=
180°-3α
180°-3α
时,仍有BQ+AQ=AB+BP.分析:(1)根据三角形内角和定理求出∠ABC的度数,再根据角平分线的定义求出∠CBQ=40°,根据等角对等边的性质可得BQ=CQ,然后过点P作PD∥BQ,求出PD=CD,再利用“角角边”证明△ABP与△ADP全等,根据全等三角形对应边相等可得AB=AD,BP=PD,从而得证;
(2)根据(1)的证明,只要是满足∠ABC=2∠ACB即可是原有结论仍然成立.
(2)根据(1)的证明,只要是满足∠ABC=2∠ACB即可是原有结论仍然成立.
解答: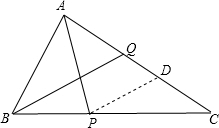 (1)证明:∵∠BAC=60°,∠ACB=40°,
(1)证明:∵∠BAC=60°,∠ACB=40°,
∴∠ABC=180°-∠BAC-∠ACB=180°-60°-40°=80°,
∵BQ平分∠ABC,
∴∠CBQ=
∠ABC=
×80°=40°,
∴∠CBQ=∠ACB,
∴BQ=CQ,
∴BQ+AQ=CQ+AQ=AC…①,
过点P作PD∥BQ交CQ于点D,
则∠CPD=∠CBQ=40°,
∴∠CPD=∠ACB=40°,
∴PD=CD,∠ADP=∠CPD+∠ACB=40°+40°=80°,
∵∠ABC=80°,
∴∠ABC=∠ADP,
∵AP平分∠BAC,
∴∠BAP=∠CAP,
∵在△ABP与△ADP中,
,
∴△ABP≌△ADP(AAS),
∴AB=AD,BP=PD,
∴AB+BP=AD+PD=AD+CD=AC…②,
由①②可得,BQ+AQ=AB+BP;
(2)解:根据(1)的证明可知,只要满足∠ABC=2∠ACB即可使原结论仍然成立,
∵∠ACB=α,
∴∠ABC=2α,
∴∠BAC=180°-3α.
故答案为:180°-3α.
 (1)证明:∵∠BAC=60°,∠ACB=40°,
(1)证明:∵∠BAC=60°,∠ACB=40°,∴∠ABC=180°-∠BAC-∠ACB=180°-60°-40°=80°,
∵BQ平分∠ABC,
∴∠CBQ=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CBQ=∠ACB,
∴BQ=CQ,
∴BQ+AQ=CQ+AQ=AC…①,
过点P作PD∥BQ交CQ于点D,
则∠CPD=∠CBQ=40°,
∴∠CPD=∠ACB=40°,
∴PD=CD,∠ADP=∠CPD+∠ACB=40°+40°=80°,
∵∠ABC=80°,
∴∠ABC=∠ADP,
∵AP平分∠BAC,
∴∠BAP=∠CAP,
∵在△ABP与△ADP中,
|
∴△ABP≌△ADP(AAS),
∴AB=AD,BP=PD,
∴AB+BP=AD+PD=AD+CD=AC…②,
由①②可得,BQ+AQ=AB+BP;
(2)解:根据(1)的证明可知,只要满足∠ABC=2∠ACB即可使原结论仍然成立,
∵∠ACB=α,
∴∠ABC=2α,
∴∠BAC=180°-3α.
故答案为:180°-3α.
点评:本题考查了全等三角形的判定与性质,三角形的内角和定理,等角对等边的性质,根据角度计算出∠ABC=2∠ACB从而求出相等的角是解题的关键.

练习册系列答案
相关题目
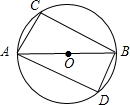 如图已知AB为⊙O的直径,弦AC∥BD,连接AD与BC.
如图已知AB为⊙O的直径,弦AC∥BD,连接AD与BC.

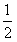 ,∠D=30°,
,∠D=30°, ,求AD的长。
,求AD的长。