题目内容
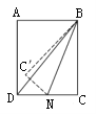
【题目】在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.
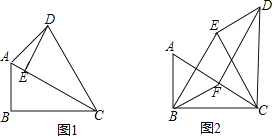
(1)当点E恰好在AC上时,如图1,求∠ADE的大小;
(2)若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.
【答案】(1)∠ADE=15°;(2)见解析.
【解析】
(1)根据旋转的性质可得CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°,根据等边对等角即可求出∠CAD=∠CDA=75°,再根据直角三角形的两个锐角互余即可得出结论;
(2)根据直角三角形斜边上的中线等于斜边的一半可得BF=![]() AC,然后根据30°所对的直角边是斜边的一半即可求出AB=
AC,然后根据30°所对的直角边是斜边的一半即可求出AB=![]() AC,从而得出 BF=AB,然后证出△ACD和△BCE为等边三角形,再利用HL证出△CFD≌△ABC,证出DF=BE,即可证出结论.
AC,从而得出 BF=AB,然后证出△ACD和△BCE为等边三角形,再利用HL证出△CFD≌△ABC,证出DF=BE,即可证出结论.
(1)解:∵△ABC绕点C顺时针旋转α得到△DEC,点E恰好在AC上,
∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°,
∴∠CAD=∠CDA=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠ADE=90°﹣∠CAD=15°;
(2)证明:如图2,连接AD
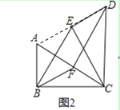
∵点F是边AC中点,
∴BF=AF=CF=![]() AC,
AC,
∵∠ACB=30°,
∴AB=![]() AC,
AC,
∴BF=CF=AB,
∵△ABC绕点C顺时针旋转60得到△DEC,
∴∠BCE=∠ACD=60°,CB=CE,DE=AB,DC=AC
∴DE=BF,△ACD和△BCE为等边三角形,
∴BE=CB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
在Rt△CFD和Rt△ABC中
![]()
∴Rt△CFD≌Rt△ABC,
∴DF=BC,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.

练习册系列答案
相关题目