题目内容
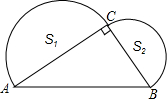 如图,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2.
如图,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2.(1)探求S1+S2的值;
(2)如果把AB=4,改为AB=a,则S1+S2的值呢?
考点:勾股定理
专题:
分析:根据半圆面积公式结合勾股定理,知S1+S2等于以斜边为直径的半圆面积.
解答:解:(1)S1=
π(
)2=
πAC2,S2=
πBC2,
所以S1+S2=
π(AC2+BC2)=
πAB2=2π.
(2)S1=
π(
)2=
πAC2,S2=
πBC2,
所以S1+S2=
π(AC2+BC2)=
πAB2=
πa2.
| 1 |
| 2 |
| AC |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
所以S1+S2=
| 1 |
| 8 |
| 1 |
| 8 |
(2)S1=
| 1 |
| 2 |
| AC |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
所以S1+S2=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
点评:考查了勾股定理.此题根据半圆的面积公式以及勾股定理证明:以直角三角形的两条直角边为直径的半圆面积和等于以斜边为直径的半圆面积,重在验证勾股定理.

练习册系列答案
相关题目
 AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么? 如图,等腰直角△OAB的直角顶点O是坐标原点,顶点在一、三象限的角平分线上,顶点B在第四象限,Rt△ODE的直角顶点E在直线OB上,且OD=4,∠ODE=30°,将Rt△ODE绕点O顺时针旋转15°,得到Rt△OD1E1,线段D1E1交直线OB于点F.若某反比例函数的图象经过点F,则这个反比例函数的解析式为
如图,等腰直角△OAB的直角顶点O是坐标原点,顶点在一、三象限的角平分线上,顶点B在第四象限,Rt△ODE的直角顶点E在直线OB上,且OD=4,∠ODE=30°,将Rt△ODE绕点O顺时针旋转15°,得到Rt△OD1E1,线段D1E1交直线OB于点F.若某反比例函数的图象经过点F,则这个反比例函数的解析式为