题目内容
(2006•杭州)如图,已知正方形ABCD的边长为2,△BPC是等边三角形,则△CDP的面积是 ;△BPD的面积是 .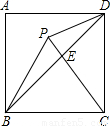
【答案】分析:因为△BPC为等边三角形,则CP=CD=2,△CDP的面积为 ×2×2sin 30°=1,S△BPD=S△BPC+S△CPD-S△BCD=
×2×2sin 30°=1,S△BPD=S△BPC+S△CPD-S△BCD= ×2×2sin60°+1-2×2×
×2×2sin60°+1-2×2× =
=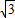 +1-2=
+1-2=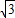 -1.
-1.
解答: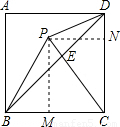 解:过P作PM⊥BC于M,PN⊥CD于N,
解:过P作PM⊥BC于M,PN⊥CD于N,
∵△BPC为等边三角形,PM⊥BC,
∴CP=CD=2,CM=BM=1,
∴PN=CM=1,
由勾股定理得:PM=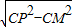 =
=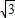 ,
,
∴△CDP的面积为 CD×PN=
CD×PN= ×2×1=1
×2×1=1
∴S△BPD=S△BPC+S△CPD-S△BCD= ×2×
×2×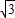 +1-2×2×
+1-2×2× =
=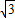 +1-2=
+1-2= -1.
-1.
点评:此题根据正四边形的性质和正三角形的形质,确定出∠PCD和∠PCB的度数,利用三角形面积公式解答.
 ×2×2sin 30°=1,S△BPD=S△BPC+S△CPD-S△BCD=
×2×2sin 30°=1,S△BPD=S△BPC+S△CPD-S△BCD= ×2×2sin60°+1-2×2×
×2×2sin60°+1-2×2× =
=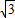 +1-2=
+1-2=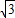 -1.
-1.解答:
 解:过P作PM⊥BC于M,PN⊥CD于N,
解:过P作PM⊥BC于M,PN⊥CD于N,∵△BPC为等边三角形,PM⊥BC,
∴CP=CD=2,CM=BM=1,
∴PN=CM=1,
由勾股定理得:PM=
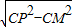 =
=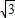 ,
,∴△CDP的面积为
 CD×PN=
CD×PN= ×2×1=1
×2×1=1∴S△BPD=S△BPC+S△CPD-S△BCD=
 ×2×
×2×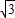 +1-2×2×
+1-2×2× =
=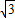 +1-2=
+1-2= -1.
-1.点评:此题根据正四边形的性质和正三角形的形质,确定出∠PCD和∠PCB的度数,利用三角形面积公式解答.

练习册系列答案
相关题目
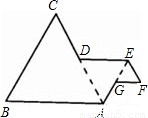
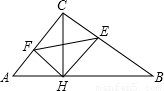
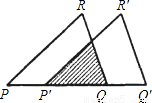
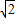 ,则此三角形移动的距离PP′是( )
,则此三角形移动的距离PP′是( )