题目内容
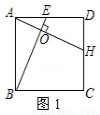
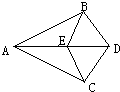20、如图，点E是AD上一点，AB=AC，（1）请你添加一个条件，使图中存在全等三角形，所添加的条件为
BE=CE
，你得到的一对全等三角形是△ABE
≌△ACE
；（2）证明（1）中的结论．
分析：本题是开放题，应先确定选择哪对三角形，再对应三角形全等条件求解．
解答：解：可选择BE=CE或∠BAD=∠CAD或BD=CD等条件中的一个．
可得到△ABE≌△ACE或△ABD≌△ACB．
证明：若添加条件为：BE=CE．
∵AB=AC，BE=CE，AE=AE，
∴△ABE≌△ACE．
故填BE=CE，△ABE≌△ACE．
可得到△ABE≌△ACE或△ABD≌△ACB．
证明：若添加条件为：BE=CE．
∵AB=AC，BE=CE，AE=AE，
∴△ABE≌△ACE．
故填BE=CE，△ABE≌△ACE．
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
练习册系列答案
相关题目
