题目内容
如图，四边形OABC为菱形，点A、B在以O为圆心的 |
| DE |
| π |
| 3 |
| π |
| 3 |
分析：连接OB，根据等边三角形的性质可以求得∠AOC=120°，再结合∠1=∠2，即可求得扇形所在的圆心角的度数，从而根据扇形的面积公式进行求解．
解答：
解：如图，连接OB，
∵OA=OB=OC=AB=BC，
∴∠AOB+∠BOC=120°．
又∵∠1=∠2，
∴∠DOE=120°，
∴S扇形ODE=
=
．
故答案为：
．
解：如图，连接OB，∵OA=OB=OC=AB=BC，
∴∠AOB+∠BOC=120°．
又∵∠1=∠2，
∴∠DOE=120°，
∴S扇形ODE=
| 120π×1 |
| 360 |
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查扇形面积的计算，同时综合运用了菱形和等边三角形的性质．掌握扇形的面积公式是解答此题的关键．
练习册系列答案
相关题目
动．过点N作NP⊥OA于点P，连接AC交NP于Q，连接MQ． 
在MN上，并与MN上的点G重合，折痕为EF，点F为折痕与y轴的交点．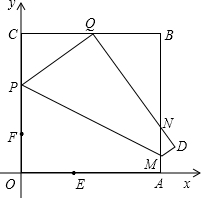
（2012•呼伦贝尔）如图，四边形OABC是边长为2的正方形，反比例函数
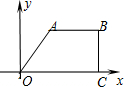是（ ）