题目内容
【题目】在平面直角坐标系xOy中，二次函数y=mx2+nx-2的图象过A（-1，-2）、B（1，0）两点．
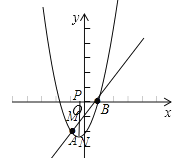
（1）求此二次函数的解析式并画出二次函数图象；
（2）点P(t,0)是x轴上的一个动点，过点P作x轴的垂线交直线AB于点M，交二次函数的图象于点N．当点M位于点N的上方时，直接写出t的取值范围．
【答案】（1）
，作图见解析；（2）-1＜t＜1．
【解析】试题分析：（1）把A（-1，-2）、B（1，0）分别代入
得到关于m、n的方程组，求出m、n即可得到二次函数的解析式，由此作出二次函数图象；
（2）观察函数图象得到当点M位于点N的上方时，M点只能在线段AB上（不含端点），则t的范围为-1＜t＜1．
试题解析：（1）把A（-1，-2）、B（1，0）分别代入
得
，解得
.
所以二次函数的解析式为
.
作图如下：
（2）-1＜t＜1．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某班25名女学生在一次“1分钟仰卧起坐”测试中，成绩如表：
成绩（次） | 43 | 45 | 46 | 47 | 48 | 49 | 51 |
人数 | 2 | 3 | 5 | 7 | 4 | 2 | 2 |
则这25名女生测试成绩的众数和中位数分别是（ ）
A.47，46
B.47，47
C.45，48
D.7，3
