题目内容
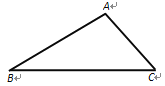
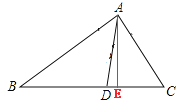
【题目】如图,在△ABC中,
(1)在图中作出△ABC的内角平分线AD.(要求:尺规作图,保留作图痕迹,不写证明过程)
(2)若∠BAC = 2∠C,在已作出的图形中,△ ∽△
(3)画出△ABC的高AE(使用三角板画出即可),若∠B=α,∠C=β,那么∠DAE= (请用含α、β的代数式表示)
【答案】(1)作图见解析;
(2)ABC,DBA;
(3)画高见解析, ![]()
【解析】试题分析:(1)考查了尺规作图能力;
(2)在△ABD与△CBA中,易证∠BAD=∠BCA,又∠B公共,根据两个角对应相等的两个三角形相似,得出△BAD∽△BCA.
(3)使用三角板画出即可.
试题解析:(1)如图,
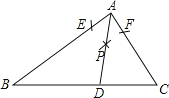
以A为圆心,任意长为半径化弧,分别交AB,AC于E,F,
然后分别以E,F为圆心,大于![]() EF的长为半径画弧,两弧交于P,
EF的长为半径画弧,两弧交于P,
作射线AP,
AD即为所求.
(2)△ABD∽△CBA理由如下:
∵AD平分∠BAC,∠BAC=2∠C,
∴∠BAD=∠BCA.
又∵∠B=∠B,
∴△ABD∽△CBA.
(3)画图如下:
∠DAE=![]()

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目