题目内容
如图，从点P向⊙O引两条切线PA，PB，切点为A，B，AC为弦，BC为⊙O的直径，若∠P=60°，PB=2cm，求AC的长．
解：连结AB．∵∠P=60°，AP=BP，
∴△APB为等边三角形．
AB=PB=2cm，PB是⊙O的切线，PB⊥BC，
∴∠ABC=30°，
∴AC=AB·tan30°=2·
=
解析:略
练习册系列答案
相关题目
如图，从点P向⊙O引两条切线PA，PB，A、B为切点，AC为弦，BC是直径．若∠P=60°，PB=2cm，求AC．
如图，从点P向⊙O引两条切线PA，PB，切点为A，B，BC为⊙O的直径，若∠P=60°，PA=3，则⊙O的直径BC的长为（ ）A、2
| ||||
B、
| ||||
| C、3 | ||||
D、4
|
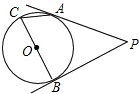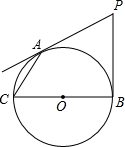如图，从点P向⊙O引两条切线PA、PB，切点A、B，BC为⊙O的直径，若∠P=60°，PA=6，求AC的长．