题目内容
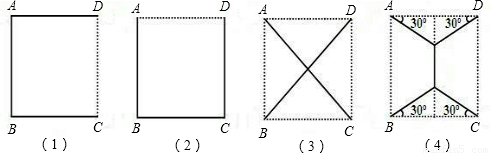
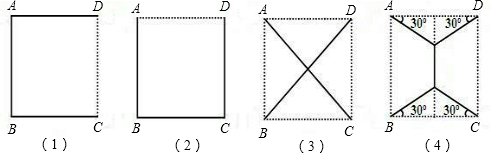
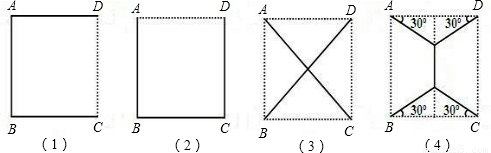
电力公司给四个村庄改造电网,这四个村庄A、B、C、D正好位于一个正方形的四个顶点,现计划在四个村庄联合架设一条线路,他们设计了四种架设方案,如图,图中的实线部分,请你帮助计算一下,哪种架设方案最省电线?(以下数据可供参考:| 2 |
| 3 |
| 5 |
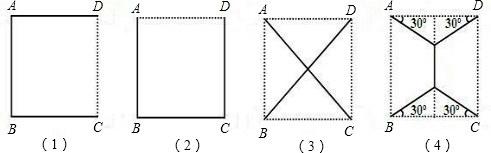
分析:分别根据4种方案,计算出电线的长度,再比较大小,找出最省电线的方案.
解答:解:设正方形边长为a.
在方案(1)中,用电线为DA+AB+BC=3a.
在方案(2)中,用电线为AB+BC+CD=3a.
在方案(3)中,用电线为AC+BD=2
a≈2.828a.
在方案(4)中,通过已知条件可知:AG=
,AE=2EG,
在Rt△AGE中,设EG=x,则AE=2x,
由勾股定理得:(2x)2=x2+(
)2,解得:x=
a,
∴EG=
a,AE=
a,
用电线为AE+DE+BF+CF+EF=4AE+(GH-2EG)=(
+1)a≈2.732a
答:方案(4)最省电线.
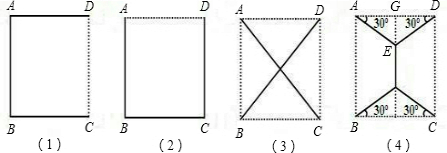
在方案(1)中,用电线为DA+AB+BC=3a.
在方案(2)中,用电线为AB+BC+CD=3a.
在方案(3)中,用电线为AC+BD=2
| 2 |
在方案(4)中,通过已知条件可知:AG=
| a |
| 2 |
在Rt△AGE中,设EG=x,则AE=2x,
由勾股定理得:(2x)2=x2+(
| a |
| 2 |
| ||
| 6 |
∴EG=
| ||
| 6 |
| ||
| 3 |
用电线为AE+DE+BF+CF+EF=4AE+(GH-2EG)=(
| 3 |
答:方案(4)最省电线.

点评:主要考查了正方形的性质和直角三角形的性质.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目

 ,
, ,
,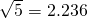 )
)
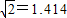 ,
,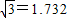 ,
,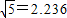 )
)
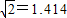 ,
,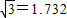 ,
,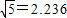 )
)