题目内容
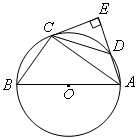
(本题10分)如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O 上,过点C的切线交AD的延长线于点E,且AE⊥CE,
连接CD.
(1)求证:DC=BC;若AB=10,AC=8,求tan∠DCE的值.
证明:
(1)连接OC.················· 1分
∵OA=OC,
∴∠OAC=∠OCA.
∵CE是⊙O的切线,
∴∠OCE=90°..············ 2分
∵AE⊥CE,
∴∠AEC=∠OCE=90°.
∴OC∥AE. . 3分
∴∠OCA=∠CAD.
∴∠CAD=∠BAC. .·· 4分
∴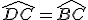 .
.
∴DC=BC. . 5分
(2)∵AB是⊙O的直径,
∴∠ACB=90°.
∴BC=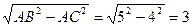 ···· 6分
···· 6分
∵∠CAE=∠BAC∠AEC=∠ACB=90°,
∴△ACE∽△ABC. 7分
∴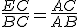 .
.
∴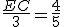
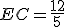 . 8分
. 8分
∵DC=BC=3,
∴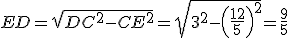 . 9分
. 9分
∴tan∠DCE=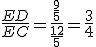 . 10分解析:
. 10分解析:
略
(1)连接OC.················· 1分
∵OA=OC,
∴∠OAC=∠OCA.
∵CE是⊙O的切线,
∴∠OCE=90°..············ 2分
∵AE⊥CE,
∴∠AEC=∠OCE=90°.
∴OC∥AE. . 3分
∴∠OCA=∠CAD.
∴∠CAD=∠BAC. .·· 4分
∴
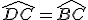 .
.
∴DC=BC. . 5分
(2)∵AB是⊙O的直径,
∴∠ACB=90°.
∴BC=
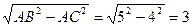 ···· 6分
···· 6分∵∠CAE=∠BAC∠AEC=∠ACB=90°,
∴△ACE∽△ABC. 7分
∴
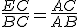 .
.∴
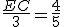
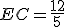 . 8分
. 8分∵DC=BC=3,
∴
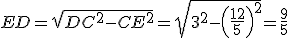 . 9分
. 9分∴tan∠DCE=
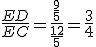 . 10分解析:
. 10分解析:略

练习册系列答案
相关题目






