ƒøƒ⁄»ð
°æƒø°ø»ÁÕº![]() £¨»Ù≈◊ŒÔœþ
£¨»Ù≈◊ŒÔœþ![]() µƒ∂•µ„
µƒ∂•µ„![]() ‘⁄≈◊ŒÔœþ
‘⁄≈◊ŒÔœþ![]() …œ£¨≈◊ŒÔœþ
…œ£¨≈◊ŒÔœþ![]() µƒ∂•µ„
µƒ∂•µ„![]() “≤‘⁄≈◊ŒÔœþ
“≤‘⁄≈◊ŒÔœþ![]() …œ£®µ„
…œ£®µ„![]() ”ε„
”ε„![]() ≤ª÷ÿ∫œ£©£¨Œ“√«∂®“£∫’‚—˘µƒ¡ΩÃı≈◊ŒÔ
≤ª÷ÿ∫œ£©£¨Œ“√«∂®“£∫’‚—˘µƒ¡ΩÃı≈◊ŒÔ![]() £¨
£¨![]() ª•Œ™°∞”—∫√°±≈◊ŒÔœþ£¨ø…º˚“ªÃı≈◊ŒÔœþµƒ°∞”—∫√°±≈◊ŒÔœþø…“‘”–∂ýÃı£Æ
ª•Œ™°∞”—∫√°±≈◊ŒÔœþ£¨ø…º˚“ªÃı≈◊ŒÔœþµƒ°∞”—∫√°±≈◊ŒÔœþø…“‘”–∂ýÃı£Æ
![]() »ÁÕº
»ÁÕº![]() £¨“—÷™≈◊ŒÔœþ
£¨“—÷™≈◊ŒÔœþ![]() ”Î
”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨ ‘«Û≥ˆµ„
£¨ ‘«Û≥ˆµ„![]() πÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒµ„
πÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
![]() «Î«Û≥ˆ“‘µ„
«Î«Û≥ˆ“‘µ„![]() Œ™∂•µ„µƒ
Œ™∂•µ„µƒ![]() µƒ”—∫√≈◊ŒÔœþ
µƒ”—∫√≈◊ŒÔœþ![]() µƒΩ‚Œˆ Ω£¨≤¢÷∏≥ˆ
µƒΩ‚Œˆ Ω£¨≤¢÷∏≥ˆ![]() ”Î
”Î![]() ÷–
÷–![]() Õ¨ ±ÀÊ
Õ¨ ±ÀÊ![]() ‘ˆ¥Û∂¯‘ˆ¥Ûµƒ◊‘±‰¡øµƒ»°÷µ∑∂Œß£ª
‘ˆ¥Û∂¯‘ˆ¥Ûµƒ◊‘±‰¡øµƒ»°÷µ∑∂Œß£ª
![]() »Ù≈◊ŒÔ
»Ù≈◊ŒÔ![]() µƒ»Œ“‚“ªÃı”—∫√≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™
µƒ»Œ“‚“ªÃı”—∫√≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™![]() £¨«Î–¥≥ˆ
£¨«Î–¥≥ˆ![]() ”Î
”Î![]() µƒπÿœµ Ω£¨≤¢Àµ√˜¿Ì”…£Æ
µƒπÿœµ Ω£¨≤¢Àµ√˜¿Ì”…£Æ

°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() £¨
£¨![]() £ª£®3£©
£ª£®3£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
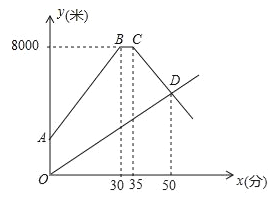
£®1£©…Ëx=0£¨«Û≥ˆyµƒ÷µ£¨º¥ø…µ√µΩCµƒ◊¯±Í£¨∞—≈◊ŒÔœþL3£∫y=2x2©Å8x+4≈‰∑Ωº¥ø…µ√µΩ≈◊ŒÔœþµƒ∂‘≥∆÷·£¨”…¥Àø…«Û≥ˆµ„Cπÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒ∂‘≥∆µ„Dµƒ◊¯±Í£ª
£®2£©”…£®1£©ø…÷™µ„Dµƒ◊¯±ÍŒ™£®4£¨4£©£¨‘Ÿ”…Ãıº˛“‘µ„DŒ™∂•µ„µƒL3µƒ°∞”—∫√°±≈◊ŒÔœþL4µƒΩ‚Œˆ Ω£¨ø…«Û≥ˆL4µƒΩ‚Œˆ Ω£¨Ω¯∂¯ø…«Û≥ˆL3”ÎL4÷–yÕ¨ ±ÀÊx‘ˆ¥Û∂¯‘ˆ¥Ûµƒ◊‘±‰¡øµƒ»°÷µ∑∂Œß£ª
£®3£©∏˘æð≈◊ŒÔœþL1µƒ∂•µ„A‘⁄≈◊ŒÔœþL2…œ£¨≈◊ŒÔœþL2µƒ∂•µ„B“≤‘⁄≈◊ŒÔœþL1…œ£¨ø…“‘¡–≥ˆ¡Ω∏ˆ∑Ω≥㨜ýº”ø…µ√£®a1+a2£©£®h©Åm£©2=0£Æø…µ√a1+a2=0£Æ
£®1£©°þ≈◊ŒÔœþL3£∫y=2x2©Å8x+4£¨°ýy=2£®x©Å2£©2©Å4£¨°ý∂•µ„Œ™£®2£¨£≠4£©£¨∂‘≥∆÷·Œ™x=2£¨…Ëx=0£¨‘Úy=4£¨°ýC£®0£¨4£©£¨°ýµ„Cπÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒ∂‘≥∆µ„Dµƒ◊¯±ÍŒ™£∫£®4£¨4£©£ª
£®2£©°þ“‘µ„D£®4£¨4£©Œ™∂•µ„µƒL3µƒ”—∫√≈◊ŒÔœþL4ªππ˝µ„£®2£¨©Å4£©£¨°ýL4µƒΩ‚Œˆ ΩŒ™y=©Å2£®x©Å4£©2+4£¨”…ÕºœÛø…÷™£¨µ±2°Ðx°Ð4 ±£¨≈◊ŒÔœþL3”ÎL4÷–yÕ¨ ±ÀÊx‘ˆ¥Û∂¯‘ˆ¥Û£ª
£®3£©a1”Îa2µƒπÿœµ ΩŒ™a1+a2=0£Æ
¿Ì”…»Áœ¬£∫
°þ≈◊ŒÔœþy=a1 £®x©Åm£©2+nµƒ“ªÃı°∞”—∫√°±≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=a2 £®x©Åh£©2+k£¨°ýy=a2 £®x©Åh£©2+kπ˝µ„£®m£¨n£©£¨«“y=a1 £®x©Åm£©2+nπ˝µ„£®h£¨k£©£¨º¥
k=a1 £®h©Åm£©2+n°≠¢Ÿ
n=a2 £®m©Åh£©2+k°≠¢⁄
”…¢Ÿ+¢⁄µ√£∫£®a1+a2£©£®h©Åm£©2=0£Æ
”÷°∞”—∫√°±≈◊ŒÔœþµƒ∂•µ„≤ª÷ÿ∫œ£¨°ýh°Ÿm£¨°ýa1+a2=0£Æ

 –°ÃÏ≤≈øŒ ±◊˜“µœµ¡–¥∞∏
–°ÃÏ≤≈øŒ ±◊˜“µœµ¡–¥∞∏ “ªøŒÀƒ¡∑œµ¡–¥∞∏
“ªøŒÀƒ¡∑œµ¡–¥∞∏ ª∆∏‘–°◊¥‘™¬˙∑÷≥¥Ì¢≤‚—Èœµ¡–¥∞∏
ª∆∏‘–°◊¥‘™¬˙∑÷≥¥Ì¢≤‚—Èœµ¡–¥∞∏ –¬∏®Ωõº—ßœµ¡–¥∞∏
–¬∏®Ωõº—ßœµ¡–¥∞∏ —Ùπ‚Õ¨—ß“ªœþ√˚ ¶»´”≈∫√æÌœµ¡–¥∞∏
—Ùπ‚Õ¨—ß“ªœþ√˚ ¶»´”≈∫√æÌœµ¡–¥∞∏