ЬтФПФкШн
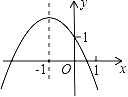
ЁОЬтФПЁПШчЭМ1,жБЯпABЗжБ№гыxжсЁЂyжсНЛгкAЁЂBСНЕу,OCЦНЗжЁЯAOBНЛABгкЕуC,ЕуDЮЊЯпЖЮABЩЯвЛЕу,Й§ЕуDзїDE//OCНЛyжсгкЕуE,вбжЊAO=m,BO=n,ЧвmЁЂnТњзуn2-12+36+|n-2m|=0.
(1)ЧѓAЁЂBСНЕуЕФзјБъ?
(2)ШєЕуDЮЊABжаЕу,ЧѓOEЕФГЄ?
(3)ШчЭМ2,ШєЕуP(x,-2x+6)ЮЊжБЯпABдкxжсЯТЗНЕФвЛЕу,ЕуEЪЧyжсЕФе§АыжсЩЯвЛЖЏЕу,вдEЮЊжБНЧЖЅЕузїЕШбќжБНЧЁїPEF,ЪЙЕуFдкЕквЛЯѓЯо,ЧвFЕуЕФКсЁЂзнзјБъЪМжеЯрЕШ,ЧѓЕуPЕФзјБъ.


ЁОД№АИЁП(1) ЕуAЮЊЃЈ3,0ЃЉЃЌЕуBЮЊЃЈ0,6ЃЉ;(2) OE=1.5;(3) ЕуPЮЊЃЈ6ЃЌ-6ЃЉ.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнЗЧИКЪ§ЕФаджЪЃЌЕУГіЗНГЬЃЈn-6ЃЉ2=0ЃЌ|n-2m|=0ЃЌЧѓЕУm=3ЃЌn=6ЃЌМДПЩЕУЕНAЁЂBСНЕуЕФзјБъЃЛЃЈ2ЃЉбгГЄDEНЛxжсгкЕуFЃЌбгГЄFDЕНЕуGЃЌЪЙЕУDG=DFЃЌСЌНгBGЃЌЙЙдьШЋЕШШ§НЧаЮЃЌдйИљОнBG=BEСаГіЙигкxЕФЗНГЬЃЌМДПЩЧѓЕУOEЕФГЄЃЛЃЈ3ЃЉЗжБ№Й§ЕуFЁЂPзїFMЁЭyжсгкЕуMЃЌPNЁЭyжсгкЕуNЃЌЩшЕуEЮЊЃЈ0ЃЌmЃЉЃЌЙЙдьШЋЕШШ§НЧаЮЃЌдйИљОнFЕуЕФКсзјБъгызнзјБъЯрЕШЃЌЕУГіЗНГЬm+2x-6=m+xЃЌНтЕУЃКx=6ЃЌМДПЩЕУЕНЕуPЮЊЃЈ6ЃЌ-6ЃЉЃЎ
БОЬтНтЮіЃК
ЃЈ1ЃЉЁп![]()
Ёр![]()
Ёп![]() ЃЌ
ЃЌ ![]()
Ёр![]() ,
,![]()
Ёр m=3ЃЌn=6
ЁрЕуAЮЊЃЈ3,0ЃЉЃЌЕуBЮЊЃЈ0,6ЃЉ
ЃЈ2ЃЉбгГЄDEНЛxжсгкЕуFЃЌбгГЄFDЕНЕуGЃЌЪЙЕУDG=DFЃЌСЌНгBG
ЩшOE=x
ЁпOCЦНЗжЁЯAOB
ЁрЁЯBOC=ЁЯAOC=45Ёу
ЁпDEЁЮOC
ЁрЁЯEFO=ЁЯFEO=ЁЯBEG=ЁЯBOC=ЁЯAOC=45Ёу
ЁрOE=OF=x
дкЁїADFКЭЁїBDGжа
Ёп
ЁрЁїADFЁеЁїBDGЃЈSASЃЉ
ЁрBG=AF=3+xЃЌЁЯG=ЁЯAFE=45Ёу
ЁрЁЯG=ЁЯBEG=45Ёу
ЁрBG=BE=6-x
Ёр6-x=3+x
НтЕУЃКx=1.5
ЁрOE=1.5
ЃЈ3ЃЉЗжБ№Й§ЕуFЁЂPзїFMЁЭyжсгкЕуMЃЌPNЁЭyжсгкЕуN
ЩшЕуEЮЊЃЈ0ЃЌmЃЉ
ЁпЕуPЕФзјБъЮЊЃЈxЃЌ-2x+6ЃЉ
дђPN=xЃЌEN=m+2x-6
ЁпЁЯPEF=90Ёу
ЁрЁЯPEN+ЁЯFEM=90Ёу
ЁпFMЁЭyжс
ЁрЁЯMFE+ЁЯFEM=90Ёу
ЁрЁЯPEN=ЁЯMFE
дкЁїEFMКЭЁїPENжа
Ёп
ЁрЁїEFMЁеЁїPENЃЈAASЃЉ
ЁрME=NP=xЃЌFM=EN=m+2x-6
ЁрЕуFЮЊЃЈm+2x-6ЃЌm+xЃЉ
ЁпFЕуЕФКсзјБъгызнзјБъЯрЕШ
Ёрm+2x-6=m+x
НтЕУЃКx=6
ЁрЕуPЮЊЃЈ6ЃЌ-6ЃЉ


 аТЛюСІзмЖЏдБЪюЯЕСаД№АИ
аТЛюСІзмЖЏдБЪюЯЕСаД№АИ СњШЫЭМЪщПьРжМйЦкЪюМйзївЕжЃжнДѓбЇГіАцЩчЯЕСаД№АИ
СњШЫЭМЪщПьРжМйЦкЪюМйзївЕжЃжнДѓбЇГіАцЩчЯЕСаД№АИЁОЬтФПЁПШчНёЃЌТУгЮЖШМйГЩЮЊСЫжаЙњШЫЧьзЃДЋЭГДКНкЕФвЛЯюЕФЁАаТФъЫзЁБЃЌЩНЮїЪЁТУЗЂЮЏЗЂВМЕФЁЖ2018ФъЁАДКНкЁБМйШеТУгЮЪаГЁзмНсЗжЮіБЈИцЁЗжаГЦЃКЩНЮїДКНкТУгЮЙЉашСНЭњЃЌЪЕЯжСЫЁАТУгЮНгД§ЁБгыЁАОМУаЇвцЁБЕФЫЋЗсЪеЃЌЧыИљОнЭМБэаХЯЂНтОіЮЪЬтЃК
ЃЈ1ЃЉШчЭМ1ЫљЪОЃЌЩНЮїНќЮхФъДКНкМйШеНгД§КЃФкЭтгЮПЭЕФЪ§СПж№ФъдіМгЃЌ2018ФъЪзДЮЭЛЦЦСЫЁАЧЇЭђЁБДѓЙиЃЌДяЕНЁЁ ЁЁЭђШЫДЮЃЌБШ2017ФъДКНкМйШедіМгЁЁ ЁЁЭђШЫДЮЃЎ
ЃЈ2ЃЉ2018Фъ2дТ15ШеЉ20ШеЦкМфЃЌЩНЮїЪЁ35ИіжиЕуОАЧјУПШеНгД§гЮПЭЪ§СПШчЯТЃК
ШеЦк | 2дТ15Ше ЃЈГ§ЯІЃЉ | 2дТ16Ше ЃЈГѕвЛЃЉ | 2дТ17Ше ЃЈГѕЖўЃЉ | 2дТ18ШеЃЈГѕШ§ЃЉ | 2дТ19Ше ЃЈГѕЫФЃЉ | 2дТ20Ше ЃЈГѕЮхЃЉ |
ШеНгД§гЮПЭЪ§СПЃЈЭђШЫДЮЃЉ | 7.56 | 82.83 | 119.51 | 84.38 | 103.2 | 151.55 |
етзщЪ§ОнЕФжаЮЛЪ§ЪЧЁЁ ЁЁЭђШЫДЮЃЎ
ЃЈ3ЃЉИљОнЭМ2жаЕФаХЯЂдЄЙРЃК2019ФъДКНкМйШеЩНЮїТУгЮзмЪеШыБШ2018ФъЭЌЦкдіГЄЕФАйЗжТЪдМЮЊЁЁ ЁЁЃЌРэгЩЪЧЁЁ ЁЁЃЎ
ЃЈ4ЃЉДКНкЦкМфЃЌаЁУїдкЁАЧрСњЙХеђЕквЛНьаТДКУэЛсЁБЩЯЙКТђСЫAЃЌBЃЌCЃЌDЫФУЖЪщЧЉЃЈГ§ЭМАИЭтЭъШЋЯрЭЌЃЉЃЎе§УцЗжБ№гЁгаЁАМєжНвеЪѕЁБЁЂЁАЙњДтОЉОчЁБЁЂЁАЬеДЩвеЪѕЁБЁЂЁАЦЄгАЯЗЁБЕФЭМАИЃЈШчЭМ3ЃЉЃЌЫћНЋЪщЧЉБГУцГЏЩЯЗХдкзРУцЩЯЃЌДгжаЫцЛњЬєбЁСНУЖЫЭИјКУХѓгбЃЌЧѓЫЭИјКУХѓгбЕФСНУЖЪщЧЉжаЧЁКУгаЁАМєжНвеЪѕЁБЕФИХТЪЃЎ