题目内容
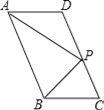
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90,当点D在线段BC上时(与点B不重合),如图2,线段CF,BD所在直线位置关系为 ,数量关系为 .
(2)如果AB=AC,∠BAC=90,当点D在线段BC的延长线时,如图3,(1)中的结论是否仍然成立,并说明理由。
(3)如果AB=AC,∠BAC是钝角,点D在线段BC上,当∠ABC满足什么条件时,CF⊥BC(点C、F不重合)画出图形,并说明理由。

【答案】(1)CF与BD位置关系是垂直,数量关系是相等(2)当点D在BC的延长线上时①的结论仍成立 (3)当∠ACB=45![]() 时
时
【解析】分析: (1)①证明△BAD≌△CAF,可得:BD=CF,∠B=∠ACF=45°,则∠BCF=∠ACB+∠ACF=90°,所以BD与CF相等且垂直;
②①的结论仍成立,同理证明△DAB≌△FAC,可得结论:垂直且相等;
(2)当∠ACB满足45°时,CF⊥BC;如图4,作辅助线,证明△QAD≌△CAF,即可得出结论.
详解:
(1)CF与BD位置关系是垂直,数量关系是相等
(2)当点D在BC的延长线上时①的结论仍成立
由正方形ADEF得AD=AF,∠DAF=90°

∵∠BAC=90v,
∴∠DAF=∠BAC,
∴∠DAB=∠FAC
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD
∠ACF=∠ABD
∵∠BAC=90°,AB=AC
∴∠ABC=45°

∴∠ACF=45°
∴∠BCF=∠ACB+∠ACF=90°
即CF⊥BD.
(3)当∠ACB=45°时,CF⊥BD,理由:
过点A作AG⊥AC交BC于点G
∴AC=AG
可证得:△GAD≌△CAF
∴∠ACF=∠AGD=45°
∠BCF=∠ACB+∠ACF=90°
即CF⊥BD.
点睛: 本题是四边形的综合题,考查了正方形、等腰直角三角形、全等三角形的性质和判定,本题的三个结论都是证明三角形全等得出,所以利用SAS证明三角形全等是本题的关键;第(2)问,恰当地作辅助线,构建等腰直角三角形,同样也是构建两个三角形全等得出结论.