Question

【题目】如图1，在平面直角坐标系中，A（a，b），B（c，0）是x轴正半轴上一点，∠ABO＝30°，若与|2﹣a|互为相反数．

（1）求c的值；

（2）如图2，AC⊥AB交x轴于C，以AC为边的正方形ACDE的对角线AD交x轴于F．

①求证：BE＝2OC；

②记BF2﹣OF2＝m，OC2＝n，求的值．

Answer 1

【答案】（1）2+2；（2）①详见解析；②3．

【解析】

（1）利用非负数的性质求出a，b的值，可得点A的坐标，如图1中，过点A作AH⊥OB于H．解直角三角形求出OH，BH即可解决问题．

（2）①如图2中，延长AC交y轴于G，过点A作AT⊥OA交OB于T．证△AOG≌△ATB（AAS），推出AG＝AB，∠AGO＝∠ABT＝30°可得结论．

②如图2中，连接GF．证明△GAF≌△BAF（SAS），推出BF＝FG可得结论．

（1）解：∵与|2﹣a|互为相反数，

又∵≥0，|2﹣a|≥0，

∴a＝b＝2，

∴A（2，2），

如图1中，过点A作AH⊥OB于H．

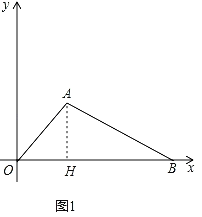
∴AH＝OH＝2，

在Rt△AHB中，∵∠AHB＝90°，AH＝2，∠ABH＝30°，

∴tan∠ABH==tan30°

∴ BH＝AH＝2，

∴OB＝2+2，

∴B（2+2，0）．

（2）①证明：如图2中，延长AC交y轴于G，过点A作AT⊥OA交OB于T．

由（1）可知∠AOB＝45°，

∵OA⊥AT，AC⊥AB，

∴∠OAT＝∠CAB＝90°，

∴∠OAG＝∠TAB，∠ATO＝∠AOT＝45°，

∴OA＝OT，

∵∠AOG＝∠ATB＝135°，

∴△AOG≌△ATB（AAS），

∴AG＝AB，∠AGO＝∠ABT＝30°，

∵四边形ACDE是正方形，

∴AC＝AE，

∵AG＝AB，

∴CG＝BE，

∵∠COG＝90°∠CGO＝30°，

∴CG＝2OC，

∴BE＝2OC．

②解：如图2中，连接GF．

∵AG＝AB，∠GAF＝∠BAF＝45°，AF＝AF，

∴△GAF≌△BAF（SAS），

∴BF＝FG，

∴m＝BF2﹣OF2＝GF2﹣OF2＝OG2，

∵OG＝OC，

∴＝＝（）2＝3．