题目内容
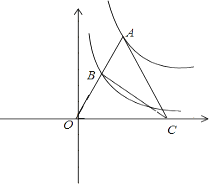
【题目】如图,正方形ABCD的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,点B在双曲线![]() (x<0)上,点D在双曲线
(x<0)上,点D在双曲线![]() (x>0)上,点D的坐标是 (3,3)
(x>0)上,点D的坐标是 (3,3)
(1)求k的值;
(2)求点A和点C的坐标.
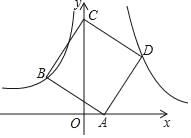
【答案】(1)k=9,(2)A(1,0), C(0,5).
【解析】
(1)根据反比例函数过点D,将坐标代入即可求值,(2)利用全等三角形的性质,计算AM,AN,CH的长即可解题.
解:将点D代入![]() 中,
中,
解得:k=9,
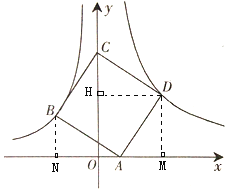
(2)过点B作BN⊥x轴于N, 过点D作DM⊥x轴于M,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵∠BAN+∠ABN=90°,
∴∠BAN=∠ADM,
∴△ABN≌△DAM(AAS),
∴DM=AN=3,
设A(a,0),
∴N(a-3,0),
∵B在![]() 上,
上,
∴BN=![]() =AM,
=AM,
∵OM=a![]() =3,整理得:a2-6a+5=0,
=3,整理得:a2-6a+5=0,
解得:a=1或a=5(舍去),
经检验,a=1是原方程的根,
∴A(1,0),
过点D作DH⊥Y轴于H,
同理可证明△DHC≌△DMA,
∴CH=AM=2,
∴C(0,5),
综上, A(1,0), C(0,5).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目