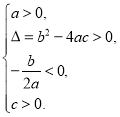题目内容
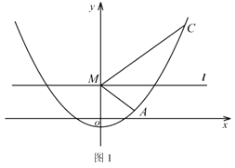
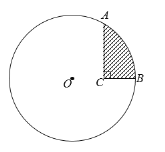
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一个动点(不与
上一个动点(不与![]() 、
、![]() 重合),点
重合),点![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,设
,设![]() .
.
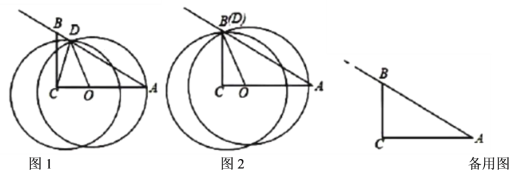
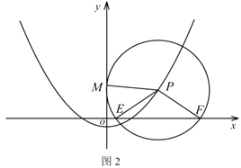
(1)如图2,当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)当点![]() 在线段
在线段![]() 上,如果
上,如果![]() 与
与![]() 的另一个交点
的另一个交点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,试求
,试求![]() 与
与![]() 之间的函数解析式,并写出
之间的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)在点![]() 的运动过程中,如果
的运动过程中,如果![]() 与线段
与线段![]() 只有一个公共点,请直接写出
只有一个公共点,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)当
;(3)当![]() 或
或![]() 或
或![]() 时,
时,![]() 与线段
与线段![]() 只有一个公共点.
只有一个公共点.
【解析】
(1)在Rt△BOC中,利用勾股定理即可解决问题.
(2)如图2中,作OH⊥AB于H,CG⊥AB于G,连接CE.证明![]() ,利用相似三角形的性质构建关系式即可解决问题.
,利用相似三角形的性质构建关系式即可解决问题.
(3)分三种情形分别求解即可解决问题.
解:(1)如图1中,
图1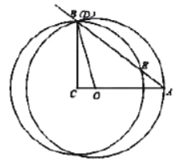
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]()
(2)过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]()
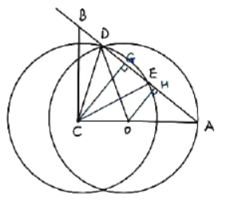
![]() ;
;![]()
![]() ;
;![]()
又![]() 在
在![]() 中
中![]() ;
;
![]() 在
在![]() 中
中![]() ;
;
![]()
∵∠AGC=∠ACB=90°,∠A=∠A,
∴![]()
![]()
![]()
又![]() ,
,![]()
![]()
又![]()
即![]()
化简得![]()
![]()
(3)①如图1中,当![]() 经过点
经过点![]() 时,
时,
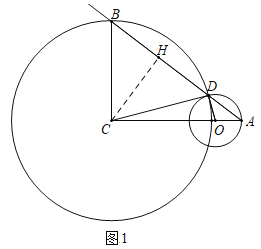
易知:![]()
![]()
![]()
![]()
![]()
观察图象可知:当![]() 时,
时,![]() 与线段
与线段![]() 只有一个公共点.
只有一个公共点.
②如图2中,当![]() 与
与![]() 相切时,
相切时,![]() ,易知
,易知![]() ,此时
,此时![]()

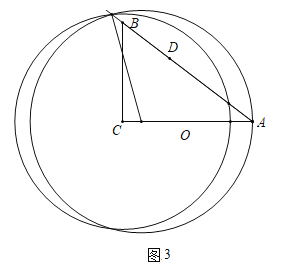
③如图3中,当![]() 时,
时,![]() 与线段
与线段![]() 只有一个公共点.
只有一个公共点.
综上所述,当![]() 或
或![]() 或
或![]() 时,
时,![]() 与线段
与线段![]() 只有一个公共点.
只有一个公共点.

练习册系列答案
相关题目
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
方程两根的情况 | 对应的二次函数的大致图象 |
|
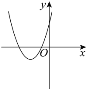
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
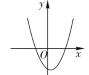
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.