题目内容
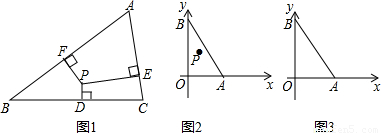
我们把三角形内部的一个点到这个三角形三边所在直线距离的最小值叫做这个点到这个三角形的距离.如图1,PD⊥BC于D,PE⊥AC于E,PF⊥AB于F,如果PE≥PF≥PD,则称PD的长度为点P到△ABC的距离.如图2、图3,在平面直角坐标系中,已知A(6,0),B(0,8),连接AB.(1)若P在图2中的坐标为(2,4),则P到OA的距离为______,P到OB的距离为______,P到AB的距离为______,所以P到△AOB的距离为______;
(2)若点Q是图2中△AOB的内切圆圆心,求点Q到△AOB距离的最大值;
(3)若点R是图3中△AOB内一点,且点R到△AOB的距离为1,请画出所有满足条件的点R所形成的封闭图形,并求出这个封闭图形的周长.(画图工具不限)
【答案】分析:(1)根据P点坐标得出P到OA,OB的距离即可,进而根据图形的面积得出P到AB的距离;
(2)根据当点Q到△AOB三边距离相等即Q为△AOB的内心时,Q到△AOB的距离最大,根据三角形面积求出即可;
(3)根据点P到三角形的距离定义得出R的移动范围,进而得出点R所形成的封闭图形形状,进而得出答案.
解答: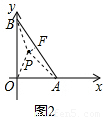 解:(1)如图2,∵P在图2中的坐标为(2,4),
解:(1)如图2,∵P在图2中的坐标为(2,4),
∴P到OA的距离为:4,
P到OB的距离为:2,
∵(6,0),B(0,8),
∴OB=8,AO=6,则AB=10,
设P到AB的距离为x,
则 ×2×BO+
×2×BO+ ×AO×4+
×AO×4+ ×AB×x=
×AB×x= ×6×8,
×6×8,
解得:x=0.8,
故P到AB的距离为:0.8,所以P到△AOB的距离为:0.8;
故答案为:4,2,0.8,0.8;
(2)当点Q到△AOB三边距离相等即Q为△AOB的内心时,
Q到△AOB的距离最大.
设这个最大值为h,则 ×8×h+
×8×h+ ×6×h+
×6×h+ ×10×h=
×10×h= ×6×8,
×6×8,
解得:h=2.
∴点Q到△AOB距离的最大值为2.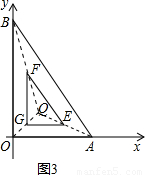
(3)设点Q为△AOB的内心,
如图3,连接QA,QB,QO,分别取QA,QB,QO的中点E,F,G,连接EF,FG,GE,
则△EFG即为所要画的图形.(只要画图正确即可,不必书写画图过程),
由画图可知,△EFG∽△ABO,
由上题及已知条件可知,△EFG与△ABO的相似比为 ,
,
因为△ABO的周长为24,所以△EFG的周长为12.
点评:此题主要考查了三角形内心的知识以及位似图形的性质,根据已知结合三角形面积公式得出Q的位置是解题关键.
(2)根据当点Q到△AOB三边距离相等即Q为△AOB的内心时,Q到△AOB的距离最大,根据三角形面积求出即可;
(3)根据点P到三角形的距离定义得出R的移动范围,进而得出点R所形成的封闭图形形状,进而得出答案.
解答:
 解:(1)如图2,∵P在图2中的坐标为(2,4),
解:(1)如图2,∵P在图2中的坐标为(2,4),∴P到OA的距离为:4,
P到OB的距离为:2,
∵(6,0),B(0,8),
∴OB=8,AO=6,则AB=10,
设P到AB的距离为x,
则
 ×2×BO+
×2×BO+ ×AO×4+
×AO×4+ ×AB×x=
×AB×x= ×6×8,
×6×8,解得:x=0.8,
故P到AB的距离为:0.8,所以P到△AOB的距离为:0.8;
故答案为:4,2,0.8,0.8;
(2)当点Q到△AOB三边距离相等即Q为△AOB的内心时,
Q到△AOB的距离最大.
设这个最大值为h,则
 ×8×h+
×8×h+ ×6×h+
×6×h+ ×10×h=
×10×h= ×6×8,
×6×8,解得:h=2.
∴点Q到△AOB距离的最大值为2.

(3)设点Q为△AOB的内心,
如图3,连接QA,QB,QO,分别取QA,QB,QO的中点E,F,G,连接EF,FG,GE,
则△EFG即为所要画的图形.(只要画图正确即可,不必书写画图过程),
由画图可知,△EFG∽△ABO,
由上题及已知条件可知,△EFG与△ABO的相似比为
 ,
,因为△ABO的周长为24,所以△EFG的周长为12.
点评:此题主要考查了三角形内心的知识以及位似图形的性质,根据已知结合三角形面积公式得出Q的位置是解题关键.

练习册系列答案
相关题目