Question

如图（1）所示，△ABC是直角三角形，BD是斜边上的高，若AB=3，BC=4，AC=5，求BD的长．
解：因为S_△ABC=

1

2

AB•BC，S_△ABC=

1

2

AC•BD，所以

1

2

AB•BC=

1

2

AC•BD，
所以3×4=5BD，则BD=

12

5

，
以上求解的基本思想是以三角形的面积不变为相等关系，通过从不同角度表示同一三角形的面积来发现三角形各边及其上的高的关系，这种解决问题的方法我们常称为“面积法”，根据你的理解回答下面的问题：
如图（2）所示，△ABC中，AD，CE都是△ABC的高，且AD=3cm，CE=2cm，AB=6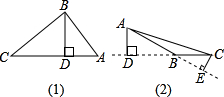cm，求CB的长．

Answer 1

分析：可通过阅读后，类比推算．按（1）给出的方法，我们可得出关于图2中BC，AD，AB，CE的比例关系，有AD，CE，AB的长，求BC就容易多了．

解答：解：因为S_△ABC=

1

2

BC•AD=

1

2

AB•CE，所以BC•AD=AB•CE，
所以3BC=6×2，则BC=4cm．

点评：本题的解题关键是要读懂题中给出的计算方法．然后类比推算即可．