题目内容
给出函数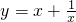 .
.
(1)写出自变量x的取值范围;
(2)请通过列表、描点、连线画出这个函数的图象;
①列表:
| x | … | -4 | -3 | -2 | -1 | - | - | - |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | … |

③连线(将上图中描出的各点用平滑曲线连接起来,得到函数图象)
(3)观察函数图象,回答下列问题:
①函数图象在第______象限;
②函数图象的对称性是(______)
A.既是轴对称图形,又是中心对称图形
B.只是轴对称图形,不是中心对称图形
C.不是轴对称图形,而是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
③在x>0时,当x=______时,函数y有最______(大,小)值,且这个最值等于______;
在x<0时,当x=______时,函数y有最______(大,小)值,且这个最值等于______;
④在第一象限内,x在什么范围内,y随着x增大而减小,x在什么范围内,y随x增
大而增大;
(4)方程
 是否有实数解?说明理由.
是否有实数解?说明理由.
解:(1)自变量x的取值范围是x≠0;
(2)①列表:
②描点、③连线:

(3)观察函数图象,回答下列问题:
①函数图象在第一、三象限;
②两个函数图象关于原点对称,那么对称性为:不是轴对称图形,而是中心对称图形;故选C.
③在x>0时,当x=1时,函数y有最小值,且这个最值等于2;
在x<0时,当x=-1时,函数y有最大值,且这个最值等于-2;
④在第一象限内,当x<1时,
y随着x增大而减小;
当x>1时,y随x增大而增大.
(4)

方程 没有实数解,
没有实数解,
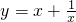 与y=-2x+1在同一直角坐标系中无交点.
与y=-2x+1在同一直角坐标系中无交点.
分析:(1)x在分母,那么x不能为0;
(2)根据所给的自变量的值得到相应的函数值,进而描点,连线即可得到相应图形;
(3)①观察所得图象看在哪两个象限即可;
②由图象可得两个函数图象只关于原点成中心对称;
③找到每个象限内图象的最低点或最高点所对应的自变量和函数值即可;
④应根据函数最低点自变量的取值判断相应变化;
(4)在同一平面直角坐标系中作出直线y=-2x+1,看有没有交点即可.
点评:用到的知识点为:分式有意义,分母不为0;函数在某个范围内的最值,看最低点或最高点所对应的自变量与函数值;两个函数解析式组成的方程无解,那么这两个函数的图象在同一坐标系中没有交点.
(2)①列表:
| x | … | -4 | -3 | -2 | -1 | - | - | - |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | - | 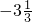 | 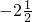 | -2 | 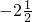 | 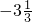 | 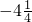 |  | 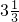 | 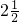 | 2 | 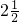 | 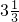 |  | … |

(3)观察函数图象,回答下列问题:
①函数图象在第一、三象限;
②两个函数图象关于原点对称,那么对称性为:不是轴对称图形,而是中心对称图形;故选C.
③在x>0时,当x=1时,函数y有最小值,且这个最值等于2;
在x<0时,当x=-1时,函数y有最大值,且这个最值等于-2;
④在第一象限内,当x<1时,
y随着x增大而减小;
当x>1时,y随x增大而增大.
(4)

方程
 没有实数解,
没有实数解,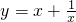 与y=-2x+1在同一直角坐标系中无交点.
与y=-2x+1在同一直角坐标系中无交点.分析:(1)x在分母,那么x不能为0;
(2)根据所给的自变量的值得到相应的函数值,进而描点,连线即可得到相应图形;
(3)①观察所得图象看在哪两个象限即可;
②由图象可得两个函数图象只关于原点成中心对称;
③找到每个象限内图象的最低点或最高点所对应的自变量和函数值即可;
④应根据函数最低点自变量的取值判断相应变化;
(4)在同一平面直角坐标系中作出直线y=-2x+1,看有没有交点即可.
点评:用到的知识点为:分式有意义,分母不为0;函数在某个范围内的最值,看最低点或最高点所对应的自变量与函数值;两个函数解析式组成的方程无解,那么这两个函数的图象在同一坐标系中没有交点.

练习册系列答案
相关题目
给出函数y=x+
.
(1)写出自变量x的取值范围;
(2)请通过列表、描点、连线画出这个函数的图象;
①列表:
②描点(在下面给出的直角坐标中描出上表对应的各点):

③连线(将上图中描出的各点用平滑曲线连接起来,得到函数图象)
(3)观察函数图象,回答下列问题:
①函数图象在第 象限;
②函数图象的对称性是( )
A.既是轴对称图形,又是中心对称图形
B.只是轴对称图形,不是中心对称图形
C.不是轴对称图形,而是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
③在x>0时,当x= 时,函数y有最 (大,小)值,且这个最值等于 ;
在x<0时,当x= 时,函数y有最 (大,小)值,且这个最值等于 ;
④在第一象限内,x在什么范围内,y随着x增大而减小,x在什么范围内,y随x增
大而增大;
(4)方程x+
=-2x+1是否有实数解?说明理由.
| 1 |
| x |
(1)写出自变量x的取值范围;
(2)请通过列表、描点、连线画出这个函数的图象;
①列表:
| x | … | -4 | -3 | -2 | -1 | -
|
-
|
-
|
|
|
|
1 | 2 | 3 | 4 | … | ||||||||||||
| y | … | … |

③连线(将上图中描出的各点用平滑曲线连接起来,得到函数图象)
(3)观察函数图象,回答下列问题:
①函数图象在第
②函数图象的对称性是(
A.既是轴对称图形,又是中心对称图形
B.只是轴对称图形,不是中心对称图形
C.不是轴对称图形,而是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
③在x>0时,当x=
在x<0时,当x=
④在第一象限内,x在什么范围内,y随着x增大而减小,x在什么范围内,y随x增
大而增大;
(4)方程x+
| 1 |
| x |
下表给出了x与函数y=x2+bx+c的一些对应值:
| x | … | 0 | 1 | 3 | 6 | … |
| y | … | 5 | 0 | -4 | 5 | … |
(2)写出抛物线y=x2+bx+c的对称轴与顶点坐标;
(3)求出y=x2+bx+c与x轴的交点坐标;
(4)画出y=x2+bx+c的大致图象,并结合图象指出,当y<0,x的取值范围.
下表给出了x与函数y=x2+bx+c的一些对应值:
(1)请根据表格求出y=x2+bx+c的解析式;
(2)写出抛物线y=x2+bx+c的对称轴与顶点坐标;
(3)求出y=x2+bx+c与x轴的交点坐标;
(4)画出y=x2+bx+c的大致图象,并结合图象指出,当y<0,x的取值范围.
| x | … | 1 | 3 | 6 | … | |
| y | … | 5 | -4 | 5 | … |
(2)写出抛物线y=x2+bx+c的对称轴与顶点坐标;
(3)求出y=x2+bx+c与x轴的交点坐标;
(4)画出y=x2+bx+c的大致图象,并结合图象指出,当y<0,x的取值范围.
给出函数 .
.
(1)写出自变量x的取值范围;
(2)请通过列表、描点、连线画出这个函数的图象;
①列表:
②描点(在下面给出的直角坐标中描出上表对应的各点):

③连线(将上图中描出的各点用平滑曲线连接起来,得到函数图象)
(3)观察函数图象,回答下列问题:
①函数图象在第______象限;
②函数图象的对称性是(______)
A.既是轴对称图形,又是中心对称图形
B.只是轴对称图形,不是中心对称图形
C.不是轴对称图形,而是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
③在x>0时,当x=______时,函数y有最______(大,小)值,且这个最值等于______;
在x<0时,当x=______时,函数y有最______(大,小)值,且这个最值等于______;
④在第一象限内,x在什么范围内,y随着x增大而减小,x在什么范围内,y随x增
大而增大;
(4)方程 是否有实数解?说明理由.
是否有实数解?说明理由.
 .
.(1)写出自变量x的取值范围;
(2)请通过列表、描点、连线画出这个函数的图象;
①列表:
| x | … | -4 | -3 | -2 | -1 | - | - | - |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | … |

③连线(将上图中描出的各点用平滑曲线连接起来,得到函数图象)
(3)观察函数图象,回答下列问题:
①函数图象在第______象限;
②函数图象的对称性是(______)
A.既是轴对称图形,又是中心对称图形
B.只是轴对称图形,不是中心对称图形
C.不是轴对称图形,而是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
③在x>0时,当x=______时,函数y有最______(大,小)值,且这个最值等于______;
在x<0时,当x=______时,函数y有最______(大,小)值,且这个最值等于______;
④在第一象限内,x在什么范围内,y随着x增大而减小,x在什么范围内,y随x增
大而增大;
(4)方程
 是否有实数解?说明理由.
是否有实数解?说明理由.