题目内容
 如图,已知:在⊙O中,直径AB=4,点E是OA上任意一点,过E作弦CD⊥AB,点F是
如图,已知:在⊙O中,直径AB=4,点E是OA上任意一点,过E作弦CD⊥AB,点F是 上一点,连接AF交CE于H,连接AC、CF、BD、OD.
上一点,连接AF交CE于H,连接AC、CF、BD、OD.
(1)求证:△ACH∽△AFC;
(2)猜想:AH•AF与AE•AB的数量关系,并说明你的猜想;
(3)探究:当点E位于何处时,S△AEC:S△BOD=1:4,并加以说明.
(1)证明:∵直径AB⊥CD,
∴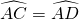 ,
,
∴∠F=∠ACH,
又∠CAF=∠FAC,
∴△ACH∽△AFC.
(2)解:AH•AF=AE•AB.
证明:连接FB,
∵AB是直径,
∴∠AFB=∠AEH=90°,
又∠EAH=∠FAB,
∴Rt△AEH∽Rt△AFB,
∴ ,
,
∴AH•AF=AE•AB.
(3)解:当 时,S△AEC:S△BOD=1:4.
时,S△AEC:S△BOD=1:4.
理由:∵直径AB⊥CD,
∴CE=ED,
∵S△AEC= AE•EC,
AE•EC,
S△BOD= OB•ED,
OB•ED,
∴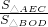 =
= =
=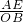 =
= ,
,
∵⊙O的半径为2,
∴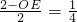 ,
,
∴8-4OE=2,
∴OE= .
.
即当点E距离点O 时S△AEC:S△BOD=1:4.
时S△AEC:S△BOD=1:4.
分析:(1)根据垂径定理得到弧AC=弧AD,再根据圆周角定理的推论得到∠F=∠ACH,根据两个角对应相等证明两个三角形相似;
(2)连接BF,构造直角三角形,把要探索的四条线段放到两个三角形中,根据相似三角形的判定和性质证明;
(3)根据三角形的面积公式,得到两个三角形的面积比即为AE:OB,进一步转化为AE:AO的比,再根据半径的长求得OE的长.
点评:能够综合运用垂径定理和圆周角定理的推论得到有关的角相等.掌握相似三角形的判定和性质.
∴
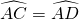 ,
,∴∠F=∠ACH,
又∠CAF=∠FAC,
∴△ACH∽△AFC.
(2)解:AH•AF=AE•AB.

证明:连接FB,
∵AB是直径,
∴∠AFB=∠AEH=90°,
又∠EAH=∠FAB,
∴Rt△AEH∽Rt△AFB,
∴
 ,
,∴AH•AF=AE•AB.
(3)解:当
 时,S△AEC:S△BOD=1:4.
时,S△AEC:S△BOD=1:4.理由:∵直径AB⊥CD,

∴CE=ED,
∵S△AEC=
 AE•EC,
AE•EC,S△BOD=
 OB•ED,
OB•ED,∴
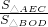 =
= =
=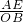 =
= ,
,∵⊙O的半径为2,
∴
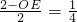 ,
,∴8-4OE=2,
∴OE=
 .
.即当点E距离点O
 时S△AEC:S△BOD=1:4.
时S△AEC:S△BOD=1:4.分析:(1)根据垂径定理得到弧AC=弧AD,再根据圆周角定理的推论得到∠F=∠ACH,根据两个角对应相等证明两个三角形相似;
(2)连接BF,构造直角三角形,把要探索的四条线段放到两个三角形中,根据相似三角形的判定和性质证明;
(3)根据三角形的面积公式,得到两个三角形的面积比即为AE:OB,进一步转化为AE:AO的比,再根据半径的长求得OE的长.
点评:能够综合运用垂径定理和圆周角定理的推论得到有关的角相等.掌握相似三角形的判定和性质.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
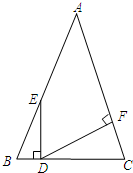 10、如图,已知:在△ABC中,AB=AC,D是BC边上任意一点,DF⊥AC于点F,E在AB边上,ED⊥BC于D,∠AED=155°,则∠EDF等于( )
10、如图,已知:在△ABC中,AB=AC,D是BC边上任意一点,DF⊥AC于点F,E在AB边上,ED⊥BC于D,∠AED=155°,则∠EDF等于( ) 11、如图,已知:在?ABCD中,AE⊥BC交BC于E,AF⊥CD交CD于F,∠EAF=60°,BE=2cm,DF=3cm,则AB=
11、如图,已知:在?ABCD中,AE⊥BC交BC于E,AF⊥CD交CD于F,∠EAF=60°,BE=2cm,DF=3cm,则AB= 如图,已知:在?ABCD中,E是BC的中点,AE交BD于F,且AE=9,BD=12,AD=10,则?ABCD的面积是
如图,已知:在?ABCD中,E是BC的中点,AE交BD于F,且AE=9,BD=12,AD=10,则?ABCD的面积是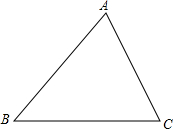 如图,已知:在△ABC中,∠BAC=75°,∠ACB=60°,AB=8
如图,已知:在△ABC中,∠BAC=75°,∠ACB=60°,AB=8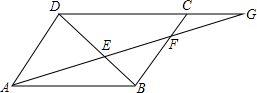 如图,已知:在?ABCD中,G是DC延长线上一点,AG分别交BD和BC于E、F.试说明AF•AD=AG•BF.
如图,已知:在?ABCD中,G是DC延长线上一点,AG分别交BD和BC于E、F.试说明AF•AD=AG•BF.