题目内容
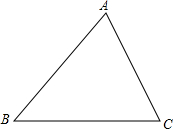如图，已知：在△ABC中，∠BAC=75°，∠ACB=60°，AB=8| 2 |
分析：过D点作AD⊥BC于D．根据30°的直角三角形的性质和等腰直角三角形的性质进行计算．
解答：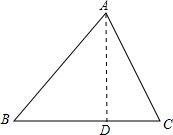
解：过D点作AD⊥BC于D．
在直角三角形ACD中，∠ACB=60°，
∴∠CAD=30°．
又∠BAC=75°，
∴∠BAD=45°．
在直角三角形ABD中，AB=8
，
∴AD=BD=8．
∴CD=AD•tan∠CAD=
．
∴BC=8+
．
解：过D点作AD⊥BC于D．在直角三角形ACD中，∠ACB=60°，
∴∠CAD=30°．
又∠BAC=75°，
∴∠BAD=45°．
在直角三角形ABD中，AB=8
| 2 |
∴AD=BD=8．
∴CD=AD•tan∠CAD=
| 8 |
| 3 |
| 3 |
∴BC=8+
| 8 |
| 3 |
| 3 |
点评：通过巧妙作高，构造特殊直角三角形，再根据特殊角的锐角三角函数值进行求解．
练习册系列答案
相关题目
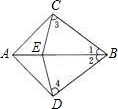
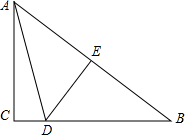如图，已知：在Rt△ABC中，∠C=90°，E为AB的中点，且DE⊥AB于E，若∠CAD：∠DAB=1﹕2，求∠B的度数．
