题目内容
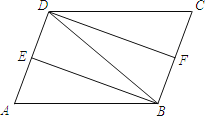
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据平行四边形性质得出AB=CD,∠A=∠C.求出∠ABD=∠CDB.推出∠ABE=∠CDF,根据ASA推出全等即可;
(2)根据全等得出AE=CF,根据平行四边形性质得出AD∥BC,AD=BC,推出DE∥BF,DE=BF,得出四边形DFBE是平行四边形,根据等腰三角形性质得出∠DEB=90°,根据矩形的判定推出即可.
试题解析:(1)在□ABCD中,AB=CD,∠A=∠C.∵AB∥CD,∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,∴∠ABE=![]() ∠ABD,∠CDF=
∠ABD,∠CDF=![]() ∠CDB,∴∠ABE=∠CDF.
∠CDB,∴∠ABE=∠CDF.
∵在△ABE和△CDF中,∵∠A=∠C,AB=DC,∠ABE=∠CDF,∴△ABE≌△CDF(ASA).
(2)∵△ABE≌△CDF,∴AE=CF,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴DE∥BF,DE=BF,∴四边形DFBE是平行四边形,∵AB=DB,BE平分∠ABD,∴BE⊥AD,即∠DEB=90°,∴平行四边形DFBE是矩形.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
班级 | 平均数(分) | 中位数 | 众数 |
九(1) | 85 | 85 | |
九(2) | 80 |
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.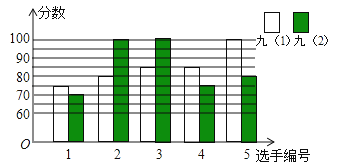
【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去租用这两种货车情况如下:
第一次 | 第二次 | |
甲种货车数量 | 2辆 | 5辆 |
乙种货车数量 | 3辆 | 6辆 |
累计运货重量 | 14吨 | 32吨 |
(1)分别求甲、乙两种货车载重多少吨?
(2)现在租用该公司5辆甲货车和7辆乙货车一次刚好运完这批货物,如果按每吨付费50元计算,货主应付运费多少元?