题目内容
如图，一次函数的图象过点P（2，3），交x轴的正半轴与A，交y轴的正半轴与B，求△AOB面积的最小值．
解：设一次函数解析式为y=kx+b，
则3=2k+b，
解得b=3-2k，
令y=0，得x=-
，则OA=-．
令x=0，得y=b，则OB=b．
S△AOB=
×（-）×b
=×
=×
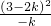
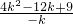
=[（2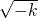
-
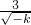）2+24]≥12．
所以，△AOB面积的最小值为12．
分析：先设出一次函数的解析式，把它与x，y轴交点的坐标用k，b表示出来，让其面积最小值转化成不等式的形式求解．
点评：本题考查的是用待定系数法求一次函数的解析式，解答时只要把A，B两点的坐标表示出来，让其面积最小值转化成不等式的形式求解即可．
则3=2k+b，
解得b=3-2k，
令y=0，得x=-
，则OA=-．令x=0，得y=b，则OB=b．
S△AOB=
×（-）×b=
×=
×=
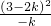
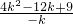
[（2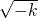-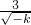）2+24]≥12．所以，△AOB面积的最小值为12．
分析：先设出一次函数的解析式，把它与x，y轴交点的坐标用k，b表示出来，让其面积最小值转化成不等式的形式求解．
点评：本题考查的是用待定系数法求一次函数的解析式，解答时只要把A，B两点的坐标表示出来，让其面积最小值转化成不等式的形式求解即可．
练习册系列答案
相关题目
如图，已知反比例函数y=
( x<0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0).当x<–1时，一次函数值大于反比例函数的值，当x>–1时，一次函数值小于反比例函数值.
(x>0)的图象与y1= – 
（x＜0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0），当x＜－1时，一次函数值大于反比例函数值，当x＞－1时，一次函数值小于反比例函数值．
（x＞0）的图象与
的坐标．
解答：
