题目内容
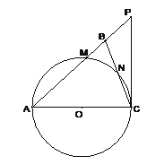
【题目】在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.
(1)圆心O到CD的距离是______;
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)
【答案】5;25+![]() -
- ![]() .
.
【解析】试题分析:(1)、连接OE,根据切线可得OE⊥CD,根据AB求出OE的长度,即圆心到CD的距离;(2)、根据平行四边形得出∠C=120°,∠BOE=90°,作EF∥CB,根据Rt△OEF求出OF的长度,然后得出EC和DE长度,从而求出梯形OADE的面积和扇形OAE的面积,从而得出阴影部分的面积.
试题解析:(1)、连接OE.
∵边CD切⊙O于点E.∴OE⊥CD 则OE就是圆心O到CD的距离,则圆心O到CD的距离是![]() ×AB=5.
×AB=5.
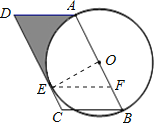
(2)∵四边形ABCD是平行四边形. ∴∠C=∠DAB=180°-∠ABC=120°,
∴∠BOE=360°-90°-60°-120°=90°, ∴∠AOE=90°,
作EF∥CB,∴∠OFE=∠ABC=60°, 在直角三角形OEF中,OE=5,
∴OF=OE![]() tan30°=
tan30°=![]() .EC=BF=5-
.EC=BF=5-![]() . 则DE=10-5+
. 则DE=10-5+![]() =5+
=5+![]() ,
,
则直角梯形OADE的面积是: ![]() (OA+DE)×OE=
(OA+DE)×OE=![]() (5+5+
(5+5+![]() )×5=25+
)×5=25+![]() .
.
扇形OAE的面积是: ![]() . 则阴影部分的面积是:25+
. 则阴影部分的面积是:25+![]() -
- ![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目