题目内容
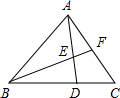 如图,三角形ABC的面积是30平方厘米,AE=ED、BD=
如图,三角形ABC的面积是30平方厘米,AE=ED、BD=| 2 | 3 |
分析:首先观察图象,发现△ABD与△ABC同高,且底边BD=
BC;△ABD与△EBD同高,且底边ED=
AD.再根据同高的三角形,面积的比等于底边的比,即可解得结果.
| 2 |
| 3 |
| 1 |
| 2 |
解答:解:∵△ABD与△ABC同高,且底边BD=
BC,
∴S△ABD=
S△ABC,
∵△ABD与△EBD同高,且底边AE=ED(即ED=
AD),
∴S△BED=
S△ABC,
∴S△ABD=
×
S△ABC=
×30=10.
故答案为:10.
| 2 |
| 3 |
∴S△ABD=
| 2 |
| 3 |
∵△ABD与△EBD同高,且底边AE=ED(即ED=
| 1 |
| 2 |
∴S△BED=
| 1 |
| 2 |
∴S△ABD=
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
故答案为:10.
点评:本题考查三角形面积的计算.解决本题的关键是发现△ABD与△ABC同高,且底边BD=
BC;△ABD与△EBD同高,且底边ED=
AD.这一特殊性.
| 2 |
| 3 |
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
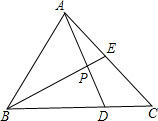 如图,三角形ABC的面积为1,BD:DC=2:1,E为AC的中点,AD与BE相交于P,那么四边形PDCE的面积为
如图,三角形ABC的面积为1,BD:DC=2:1,E为AC的中点,AD与BE相交于P,那么四边形PDCE的面积为 (2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.
(2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.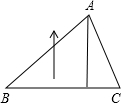 如图,三角形ABC的底边BC长3厘米,BC边上的高是2厘米,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,这时,三角形扫过的面积是多少平方厘米( )
如图,三角形ABC的底边BC长3厘米,BC边上的高是2厘米,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,这时,三角形扫过的面积是多少平方厘米( )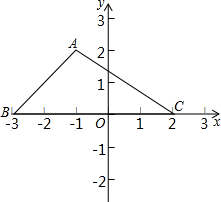 如图,三角形ABC的顶点坐标分别是A(-1,2),B(-3,0),C(2,0),求△ABC的面积.
如图,三角形ABC的顶点坐标分别是A(-1,2),B(-3,0),C(2,0),求△ABC的面积.