题目内容
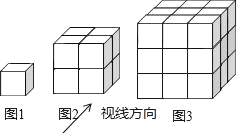
【题目】如图所示,每个小立方体的棱长为1,按如图所示的视线方向看,图1中共有1个1立方体,其中1个看得见,0个看不见;图2中共有8个立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;…,则第11个图形中,其中看得见的小立方体个数是( )
A. 271 B. 272 C. 331 D. 332
【答案】C
【解析】
根据图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
归纳出变化规律:
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,将第11个代入即可求解.
图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,
所以则第11个图形中,其中看得见的小立方体有113-103=331个,
故选C.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目