Question

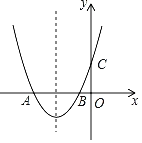
【题目】如图，在平面直角坐标系中，二次函数y＝ax2+4x﹣3图象的顶点是A，与x轴交于B，C两点，与y轴交于点D．点B的坐标是（1，0）．

（1）求A，C两点的坐标，并根据图象直接写出当y＞0时x的取值范围．

（2）平移该二次函数的图象，使点D恰好落在点A的位置上，求平移后图象所对应的二次函数的表达式．

Answer 1

【答案】（1）A（2，1），C（3，0），当y＞0时，1＜x＜3；（2）y＝﹣（x﹣4）2+5

【解析】

（1）把点B坐标代入抛物线的解析式即可求出a的值，把抛物线的一般式化为顶点式即可求出点A的坐标，根据二次函数的对称性即可求出点C的坐标，二次函数的图象在x轴上方的部分对应的x的范围即为当y＞0时x的取值范围；

（2）先由点D和点A的坐标求出抛物线的平移方式，再根据抛物线的平移规律：上加下减，左加右减解答即可．

解：（1）把B（1，0）代入y＝ax2+4x﹣3，得0＝a+4﹣3，解得：a＝﹣1，

∴y＝﹣x2+4x﹣3＝﹣（x﹣2）2+1，

∴A（2，1），

∵抛物线的对称轴是直线x＝2，B、C两点关于直线x＝2对称，

∴C（3，0），

∴当y＞0时，1＜x＜3；

（2）∵D（0，﹣3），A（2，1），

∴点D平移到点A，抛物线应向右平移2个单位，再向上平移4个单位，

∴平移后抛物线的解析式为y＝﹣（x﹣4）2+5．