Question

【题目】已知一次函数y1=ax+b的图象与反比例函数y2=的图象相交于A、B两点，坐标分别为（—2，4）、（4，—2）．

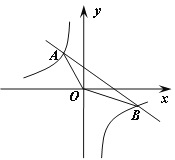
（1）求两个函数的解析式；

（2）求△AOB的面积；

（3）直线AB上是否存在一点P（A除外），使△ABO与以B﹑P、O为顶点的三角形相似？若存在，直接写出顶点P的坐标．

Answer 1

【答案】（1）y=-x+2 ，y=；（2）AOB的面积为6；（3）（，）．

【解析】

（1）将点（－2，4）、（4，－2）代入y1=ax+b，得，解得：，

∴y=-x+2 ，

将点（－2，4）代入y2=，得k＝－8，

∴y=；

（2）在y=-x+2中，当y＝0时，x＝2，

所以一次函数与x轴交点是（2，0），

故△AOB的面积为=；

（3）∵OA＝OB＝，

∴△OAB是等腰三角形，

∵△ABO与△BPO相似，

∴△BPO也是等腰三角形，

故只有一种情况，即P在OB的垂直平分线上，

设P（x，-x+2）

则，

解得：，

∴顶点P的坐标为（，）.