题目内容
 已知△ABC在直角坐标系内的位置如图,则A关于y轴的对称点坐标为
已知△ABC在直角坐标系内的位置如图,则A关于y轴的对称点坐标为(-2,4)
(-2,4)
;△ABC是等腰直角
等腰直角
三角形(形状);直线AB表示的一次函数为y=x+2
y=x+2
.分析:根据关于y轴对称的点的横坐标互为相反数,纵坐标相同解答;
根据勾股定理列式求出AB2、BC2,再利用勾股定理逆定理证明;
利用待定系数法求一次函数解析式解答即可.
根据勾股定理列式求出AB2、BC2,再利用勾股定理逆定理证明;
利用待定系数法求一次函数解析式解答即可.
解答:解:∵点A的坐标为(2,4),
∴点A关于y轴的对称点坐标为(-2,4);
根据勾股定理,AB2=22+22=8,BC2=22+22=8,AC2=42=16,
∵AB2+BC2=AC2,
∴△ABC是等腰直角三角形;
设直线AB的解析式为y=kx+b,
∵点A(2,4)B(0,2),
∴
,
解得
,
所以,直线AB的解析式为y=x+2.
故答案为:(-2,4);等腰直角;y=x+2.
∴点A关于y轴的对称点坐标为(-2,4);
根据勾股定理,AB2=22+22=8,BC2=22+22=8,AC2=42=16,
∵AB2+BC2=AC2,
∴△ABC是等腰直角三角形;
设直线AB的解析式为y=kx+b,
∵点A(2,4)B(0,2),
∴
|
解得
|
所以,直线AB的解析式为y=x+2.
故答案为:(-2,4);等腰直角;y=x+2.
点评:本题考查了待定系数法求一次函数解析式,关于y轴对称的点的坐标特征,勾股定理、勾股定理逆定理的应用,根据网格结构找出相应点的坐标是解题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 6、已知△ABC在直角坐标系中的位置如下图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )
6、已知△ABC在直角坐标系中的位置如下图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( ) 已知△ABC在直角坐标系中的位置如右图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为
已知△ABC在直角坐标系中的位置如右图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为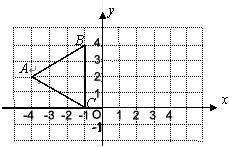 (2006•青岛)已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )
(2006•青岛)已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( ) 如图,已知△ABC在直角坐标系中.
如图,已知△ABC在直角坐标系中.