题目内容
如图①,等腰梯形ABCD中,AB∥CD,AB=4,CD=9,∠C=60°.(1)求AD的长;
(2)若动点P从点C出发沿CD方向向终点D运动(如图②),在P点运动的过程中,△ABP的面积改变了吗?若改变,请说明理由;若没有改变,那么△ABP的面积为
(3)在(2)的条件下,过B作BH⊥AP于H(如图③),若BH=2
| 2 |
(4)在(2)的条件下,若动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中一个动点到达终点时,另一个动点也随之停止运动,过点Q作QM∥CD交BC于M(如图④),探究:四边形PDQM可能为菱形吗?若可能,请求出BM的长;若不可能,请说明理由.
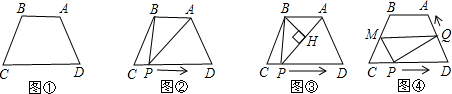
分析:(1)过点A作AE∥BC,可以得出ABCE是平行四边形,即得出AE=BC,继而得出△AED是正三角形,有AB=4,CD=9,可以得出答案.
(2)过点A作AE⊥CD于点E,作图可以得出∠2=30°,根据三角函数的性质以及勾股定理可以分别求出ED和AE的数值,有AB的值,根据面积公式求解即可.
(3)△ABP的面积有两种表示方法,根据(2)中求得的面积,又知道BH的长度,即可得出AP的值.
(4)作出图形,由MQ∥PD,得出当MQ=PD时,四边形PDQM是平行四边形,当QD=PD时,四边形PDQM是菱形,进而得出∠1=∠C=60°,即△CMP和△DPQ均为正三角形,可以求得CM=CP=4.5,过点B作BE∥AD交CD于点E,则四边形ABED是平行四边形,得出△BCE是正三角形,进而得出当MQ=PD=QD时,四边形PDQM是菱形,此时BM的长为0.5.
(2)过点A作AE⊥CD于点E,作图可以得出∠2=30°,根据三角函数的性质以及勾股定理可以分别求出ED和AE的数值,有AB的值,根据面积公式求解即可.
(3)△ABP的面积有两种表示方法,根据(2)中求得的面积,又知道BH的长度,即可得出AP的值.
(4)作出图形,由MQ∥PD,得出当MQ=PD时,四边形PDQM是平行四边形,当QD=PD时,四边形PDQM是菱形,进而得出∠1=∠C=60°,即△CMP和△DPQ均为正三角形,可以求得CM=CP=4.5,过点B作BE∥AD交CD于点E,则四边形ABED是平行四边形,得出△BCE是正三角形,进而得出当MQ=PD=QD时,四边形PDQM是菱形,此时BM的长为0.5.
解答:解:(1)过点A作AE∥BC交CD于点E,则四边形ABCE是平行四边形,
∴AE=BC,
∵等腰梯形ABCD中,AD=BC,
∴AE=AD,
∵∠1=∠C=60°,
∴△AED是正三角形,
∴AD=DE,
∵CE=AB=4,CD=9,
∴ED=DC-DE=5,
∴AD=5.
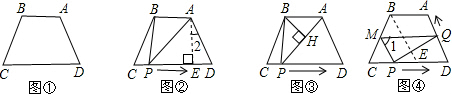
(2)△ABP的面积不变,理由:过点A作AE⊥CD于点E,
由(1)得正△ADE中∠D=60°,
∴∠2=90°-∠D=30°,
∴ED=
AD=
,
∴AE=
=
.
∴S△ABP=
AB•AE=5
.
故△ABP的面积为5
.
(3)由(2)得S△ABP=5
,而BH⊥AP,
∴
AP•BH=5
.
∵BH=2
,
∴AP=
.
(4)当MQ=PD=QD时,四边形PDQM是菱形,此时BM的长为0.5.
理由:∵MQ∥PD,
∴当MQ=PD时,四边形PDQM是平行四边形,
∴当QD=PD时,四边形PDQM是菱形,
∴MP∥=QD,
∴∠1=∠D.
∵等腰梯形中,∠D=∠C=60°,
∴∠1=∠C=60°,
∴△CMP和△DPQ均为正三角形,且边长相等.
∴CP=PD=
CD=4.5,
∴CM=CP=4.5.
过点B作BE∥AD交CD于点E,则四边形ABED是平行四边形,
∴BE=AD.
∵BC=AD,
∴BC=BE,
∴△BCE是正三角形,
∴BC=CE,
∵ED=AB=4,CD=9,
∴BC=CE=CD-AB=5,
∴BM=BC-CM=0.5.
∴AE=BC,
∵等腰梯形ABCD中,AD=BC,
∴AE=AD,
∵∠1=∠C=60°,
∴△AED是正三角形,
∴AD=DE,
∵CE=AB=4,CD=9,
∴ED=DC-DE=5,
∴AD=5.

(2)△ABP的面积不变,理由:过点A作AE⊥CD于点E,
由(1)得正△ADE中∠D=60°,
∴∠2=90°-∠D=30°,
∴ED=
| 1 |
| 2 |
| 5 |
| 2 |
∴AE=
| AD2-DE2 |
| 5 |
| 2 |
| 3 |
∴S△ABP=
| 1 |
| 2 |
| 3 |
故△ABP的面积为5
| 3 |
(3)由(2)得S△ABP=5
| 3 |
∴
| 1 |
| 2 |
| 3 |
∵BH=2
| 2 |
∴AP=
| 5 |
| 2 |
| 6 |
(4)当MQ=PD=QD时,四边形PDQM是菱形,此时BM的长为0.5.
理由:∵MQ∥PD,
∴当MQ=PD时,四边形PDQM是平行四边形,
∴当QD=PD时,四边形PDQM是菱形,
∴MP∥=QD,
∴∠1=∠D.
∵等腰梯形中,∠D=∠C=60°,
∴∠1=∠C=60°,
∴△CMP和△DPQ均为正三角形,且边长相等.
∴CP=PD=
| 1 |
| 2 |
∴CM=CP=4.5.
过点B作BE∥AD交CD于点E,则四边形ABED是平行四边形,
∴BE=AD.
∵BC=AD,
∴BC=BE,
∴△BCE是正三角形,
∴BC=CE,
∵ED=AB=4,CD=9,
∴BC=CE=CD-AB=5,
∴BM=BC-CM=0.5.
点评:本题考查了等腰梯形的性质,要能够清楚地弄懂题意,合理的作出辅助线是做题的关键.

练习册系列答案
相关题目
 1、如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=AB.点E,F分别在AD,AB上,AE=BF,DF与CE相交于P,则∠DPE=
1、如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=AB.点E,F分别在AD,AB上,AE=BF,DF与CE相交于P,则∠DPE= (2005•闸北区二模)已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:
(2005•闸北区二模)已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证: (2013•老河口市模拟)如图,在等腰梯形ABCD中,AD∥BC,AB=AD,BC=(
(2013•老河口市模拟)如图,在等腰梯形ABCD中,AD∥BC,AB=AD,BC=( 点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒:
点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒:
