题目内容
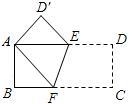 如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A、C重合,若其长BC为a,宽AB为b,则折叠后不重合部分的面积是多少?
如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A、C重合,若其长BC为a,宽AB为b,则折叠后不重合部分的面积是多少?
分析:设BF=x,则FC=a-x,根据折叠的性质得到FC=FA=a-x,在Rt△ABF中,利用勾股定理得b2+x2=(a-x)2,解出x,然后利用三角形的面积公式即可计算出△ABF的面积,易证Rt△ABF≌Rt△AD′E,所以折叠后不重合部分的面积=2S△ABF.
解答:解:设BF=x,则FC=a-x,
∵长方形纸片ABCD折叠起来,使其对角顶点A、C重合,
∴FC=FA=a-x,∠AFE=∠CFE,DC=AD′,
在Rt△ABF中,AB2+BF2=AF2,即b2+x2=(a-x)2,解得x=
,
∴S△ABF=
•AB•BF=
•b•
=
.
又∵∠AEF=∠CFE,
∴∠AFE=∠AEF,
∴AF=AE,
而AD′=DC=AB,
∴Rt△ABF≌Rt△AD′E,
所以折叠后不重合部分的面积=2S△ABF=
.
∵长方形纸片ABCD折叠起来,使其对角顶点A、C重合,
∴FC=FA=a-x,∠AFE=∠CFE,DC=AD′,
在Rt△ABF中,AB2+BF2=AF2,即b2+x2=(a-x)2,解得x=
| a2-b2 |
| 2a |
∴S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
| a2-b2 |
| 2a |
| a2b-b3 |
| 4a |
又∵∠AEF=∠CFE,
∴∠AFE=∠AEF,
∴AF=AE,
而AD′=DC=AB,
∴Rt△ABF≌Rt△AD′E,
所以折叠后不重合部分的面积=2S△ABF=
| a2b-b3 |
| 2a |
点评:本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应线段相等.也考查了三角形全等的性质与判定以及矩形的性质.

练习册系列答案
相关题目
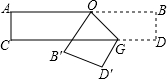 如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=70°,则∠B′OG的度数为
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=70°,则∠B′OG的度数为
 如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若∠AOB′=85°,则∠CGO的度数为
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若∠AOB′=85°,则∠CGO的度数为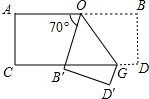 如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若∠AOB′=70°,则∠B′OG的度数为
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若∠AOB′=70°,则∠B′OG的度数为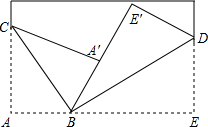 如图,将一张长方形纸斜折过去,使顶点A落在A’处,BC为折痕,然后再把BE折过去,使之与BA’重合,折痕为BD,求两折痕BC、BD的夹角∠CBD是多少度?
如图,将一张长方形纸斜折过去,使顶点A落在A’处,BC为折痕,然后再把BE折过去,使之与BA’重合,折痕为BD,求两折痕BC、BD的夹角∠CBD是多少度?