题目内容
【题目】如图，⊙O为ABC的外接圆，D为OC与AB的交点，E为线段OC延长线上一点，且EACABC.
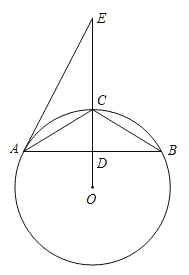
（1）求证：直线AE是⊙O的切线；
（2）若D为AB的中点，CD3，AB8.
①求⊙O的半径；②求ABC的内心I到点O的距离.
【答案】（1）见解析；（2）①⊙O的半径
；②ABC的内心I到点O的距离为
.
【解析】
（1）连接AO，证得EACABC=
,
，则EAO=EAC+CAO=
，从而得证；
（2）①设⊙O的半径为r,则OD=r-3，在△AOD中，根据勾股定理即可得出②作出ABC的内心I，过I作AC,BC的垂线，垂足分别为F,G.设内心I到各边的距离为a，由面积法列出方程求解可得答案。
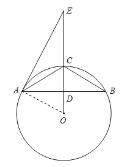
(1)如图，连接AO
则EACABC=.
又∵AO=BO,
∴ACO=CAO=
∴EAO=EAC+CAO=
AOC +
=
∴EA⊥AO
∴直线AE是⊙O的切线；
（2）①设⊙O的半径为r,则OD=r-3，
∵D为AB的中点，
∴OC⊥AB，ADO=，AD=4
∴
,即
解得
②如下图，
∵D为AB的中点，
∴
且CO是
的平分线，则内心I在CO上，连接AI,BI,过I作AC,BC的垂线，垂足分别为F,G.
易知DI=FI=GI,设其长为a.由面积可知：
即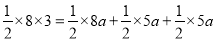
解得
∴
∴ABC的内心I到点O的距离为
【题目】某原料仓库一天的原料进出记录如下表（运进用正数表示，运出用负数表示）；
每次进出数量（单位：吨） | -3 | 4 | -1 | 2 | -5 |
进出次数 | 2 | 1 | 3 | 3 | 2 |
（1）这天仓库的原料比原来增加或减少了多少吨？
（2）根据实际情况，现有两种方案：
方案一：运进每吨原料费用5元，运出每吨原料费用8元；
方案二：不管运进还是运出费用都是每吨原料6元；
从节约运费的角度考虑，选用哪一种方案较合适？请说明理由.
【题目】某校组织七年级学生体育健康抽测，（1）班25名学生的成绩（满分为100分）统计如下：
90，74，88，65，98，76，81，42，85，70，55，80，95，88，72，87，61，56，76，66，78，72，82，63，100.
（1）90分及以上为A级，75-89分为B级，60-74分为C级，60分以下为D级，请把下面表格补充完整，并将图中的条形图补充完整；
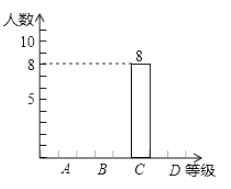
等级 | A | B | C | D |
人数 | 8 |
（2）该校七年级共有1000名学生，如果60分以上为合格，请估计七年级有多少人合格？
（3）请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.
