题目内容
已知一次函数y1=x,二次函数y2=| 1 |
| 2 |
| 1 |
| 2 |
(1)根据表中给出的x的值,填写表中空白处的值;
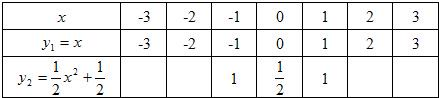
(2)观察上述表格中的数据,对于x的同一个值,判断y1和y2的大小关系.并证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1和y2的大小关系仍然成立;
(3)若把y=x换成与它平行的直线y=x+k(k为任意非零实数),请进一步探索:当k满足什么条件时,(2)中的结论仍然成立?当k满足什么条件时,(2)中的结论不能对任意的实数x都成立?并确定使(2)中的结论不成立的x的范围.
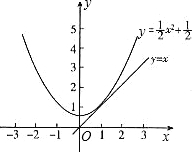
分析:(1)把x的值代入二次函数解析式,可直接求出对应的y的值.
(2)通过观察表中的数据,可得,y1≤y2,用y2-y1所得的式子进行分析,因为等于
(x-1)2,不论x取何值,都有
(x-1)2≥0,故有y2-y1≥0,即y2≥y1.
(3)解两个函数解析式组成的方程组,得到关于x的一元二次方程,根据根的判别式进行分析,(△=8k),当k<0时,一次函数的图象在二次函数的图象的下方,那么就有y2≥y1,而当k>0,时,二次函数的图象有一部分在一次函数图象的上方,一部分在下方,故这种情况不能使(2)中的结论成立.
(2)通过观察表中的数据,可得,y1≤y2,用y2-y1所得的式子进行分析,因为等于
| 1 |
| 2 |
| 1 |
| 2 |
(3)解两个函数解析式组成的方程组,得到关于x的一元二次方程,根据根的判别式进行分析,(△=8k),当k<0时,一次函数的图象在二次函数的图象的下方,那么就有y2≥y1,而当k>0,时,二次函数的图象有一部分在一次函数图象的上方,一部分在下方,故这种情况不能使(2)中的结论成立.
解答: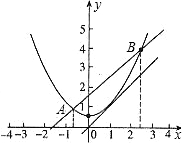 解:(1)x=-3时,y2=5;
解:(1)x=-3时,y2=5;
x=-2时,y2=
;
x=2时,y2=
;
x=3时,y2=5.
(2)y1≤y2
∵y2-y1=(
x2+
)-x=
(x-1)2
又∵x取任意实数时,都有(x-1)2≥0,
∴y2≥y1对任意的实数x都成立.
(3)由
,
得
x2+
=x+k,
即x2-2x+1-2k=0 ①
方程①的判别式△=4-4(1-2k)=8k,(k≠0)
①当k<0时,方程①无实数根,
即直线y=x+k与抛物线无交点,且直线在抛物线的下方,此时(2)中的结论仍然成立.
②当k>0时,方程①有两个不相等的实数根:x1=1-
k,x2=1+
,
即直线与抛物线有两个不同的交点,此时抛物线上有一部分点在直线的下方,
所以(2)中的结论不能对任意的x都成立.
当1-
k<1+
时,(2)中的结论不成立.
 解:(1)x=-3时,y2=5;
解:(1)x=-3时,y2=5;x=-2时,y2=
| 5 |
| 2 |
x=2时,y2=
| 5 |
| 2 |
x=3时,y2=5.
(2)y1≤y2
∵y2-y1=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵x取任意实数时,都有(x-1)2≥0,
∴y2≥y1对任意的实数x都成立.
(3)由
|
得
| 1 |
| 2 |
| 1 |
| 2 |
即x2-2x+1-2k=0 ①
方程①的判别式△=4-4(1-2k)=8k,(k≠0)
①当k<0时,方程①无实数根,
即直线y=x+k与抛物线无交点,且直线在抛物线的下方,此时(2)中的结论仍然成立.
②当k>0时,方程①有两个不相等的实数根:x1=1-
| 2 |
| 2k |
即直线与抛物线有两个不同的交点,此时抛物线上有一部分点在直线的下方,
所以(2)中的结论不能对任意的x都成立.
当1-
| 2 |
| 2k |
点评:本题利用了任何一个数的平方都是一个非负数,解方程组,一元二次方程根的判别式等知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 2,4)、(4,-2).
2,4)、(4,-2).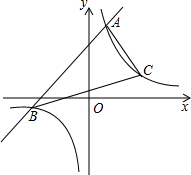 (2012•德阳)已知一次函数y1=x+m的图象与反比例函数
(2012•德阳)已知一次函数y1=x+m的图象与反比例函数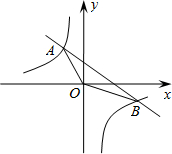 已知一次函数y1=ax+b的图象与反比例函数y2=
已知一次函数y1=ax+b的图象与反比例函数y2=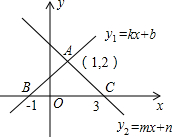 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )