题目内容
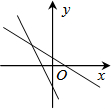
(本题满分12分)已知:如图一次函数y= x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)

(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
 x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
(1)y=
 x2-
x2- x+1
x+1(2)

(3)P的坐标为(1,0)或(3,0)
解:(1)将B(0,1),D(1,0)的坐标代入y= x2+bx+c得
x2+bx+c得
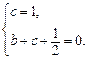 得解析式y=
得解析式y= x2-
x2- x+1……………………………………………………3分
x+1……………………………………………………3分
(2)设C(x0,y0),则有
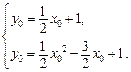 解得
解得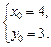 ∴C(4,3).……………………………………………6分
∴C(4,3).……………………………………………6分
由图可知:S=S△ACE-S△ABD.又由对称轴为x= 可知E(2,0).
可知E(2,0).
∴S= AE·y0-
AE·y0- AD×OB=
AD×OB= ×4×3-
×4×3- ×3×1=
×3×1= …………………………………8分
…………………………………8分
(3)设符合条件的点P存在,令P(a,0):
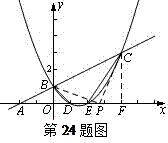
当P为直角顶点时,如图:过C作CF⊥x轴于F.
∵Rt△BOP∽Rt△PFC,∴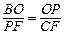 .即
.即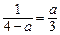 .
.
整理得a2-4a+3=0.解得a=1或a=3
∴所求的点P的坐标为(1,0)或(3,0)
综上所述:满足条件的点P共有二个………………………………………………………12分
 x2+bx+c得
x2+bx+c得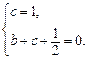 得解析式y=
得解析式y= x2-
x2- x+1……………………………………………………3分
x+1……………………………………………………3分(2)设C(x0,y0),则有
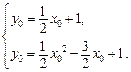 解得
解得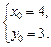 ∴C(4,3).……………………………………………6分
∴C(4,3).……………………………………………6分由图可知:S=S△ACE-S△ABD.又由对称轴为x=
 可知E(2,0).
可知E(2,0).∴S=
 AE·y0-
AE·y0- AD×OB=
AD×OB= ×4×3-
×4×3- ×3×1=
×3×1= …………………………………8分
…………………………………8分(3)设符合条件的点P存在,令P(a,0):

当P为直角顶点时,如图:过C作CF⊥x轴于F.
∵Rt△BOP∽Rt△PFC,∴
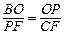 .即
.即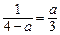 .
.整理得a2-4a+3=0.解得a=1或a=3
∴所求的点P的坐标为(1,0)或(3,0)
综上所述:满足条件的点P共有二个………………………………………………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比,燃烧后,y与x成反比(如图所示),现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为16mg。根据以上信息解答下列问题:
阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比,燃烧后,y与x成反比(如图所示),现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为16mg。根据以上信息解答下列问题: 
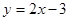 的图象不经过( )
的图象不经过( ) 与大气压强x(kpa)成正比例函数关系.当
与大气压强x(kpa)成正比例函数关系.当 时,
时, ,则
,则 与
与 的函数关系式是
的函数关系式是