题目内容
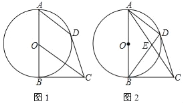
【题目】如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD
(1)求证:CD是⊙O的切线;
(2)如图2,连AC交BD于E.若AE=CE,求tan∠ACB的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)欲证明CD是⊙O的切线,只要证明∠ODC=90°,只要证明△OCD≌△OCB即可.
(2)如图2中,连接OC交BD于点M,连接OE,设EM=a,BM=2a,利用△EOM∽△EBO,得EO2=EMEB,求出EO、EB即可解决问题.
(1)证明:如图1中,连接BD、OD,BD与OC交于点E.

∵AB是直径,
∴∠ADB=90°,
∴AD⊥BD,
∵AD∥OC,
∴OC⊥BD,ED=BE,
∵OD=OB,
∴∠DOC=∠BOC,
∵BC是⊙O切线,
∴OB⊥BC,
∴∠OBC=90°,
在△OCD和△OCB中,
 ,
,
∴△OCD≌△OCB,
∴∠ODC=∠OBC=90°,
∴OD⊥CD,
∴CD是⊙O切线.
(2)如图2中,连接OC交BD于点M,连接OE,

∵AO=OB,AE=EC,
∴OE∥BC,OE=![]() BC,
BC,
∴![]() ,设EM=a,BM=2a,∠AOE=∠ABC=90°,
,设EM=a,BM=2a,∠AOE=∠ABC=90°,
∵∠OEM=∠OEB,∠OME=∠EOB=90°,
∴△EOM∽△EBO,
∴EO2=EMEB=a3a
∴EO=![]() a,
a,
同理BO2=BMBE=6a2,
∴BO=AO=![]() a,
a,
∵∠AEO=∠ACB,
∴tan∠ACB=tan∠AEO=![]() .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目





