题目内容
 28、点D是不等边三角形ABC的边AB上的一点,过点D作一条直线,使它与另一边相交截得的三角形与△ABC相似,这样的直线可以作几条?为什么?
28、点D是不等边三角形ABC的边AB上的一点,过点D作一条直线,使它与另一边相交截得的三角形与△ABC相似,这样的直线可以作几条?为什么?分析:这样的直线可以作4条,根据平行线分线段成比例定理推出相似,根据两角分别相等得到两三角形相似.
解答:解:这样的直线可以作4条.理由是:
(1)若该直线与AC相交,
①过点D作DE∥BC,交AC于点E,则∠AED=∠C,
∵∠A=∠A,
∴△ADE∽△ABC.
②过点D作直线DF交AC于点F,使得∠ADF=∠C,
∵∠A=∠A,
∴△AFD∽△ABC.
(2)同理,若该直线与BC相交,也可作①DG∥AC,②∠BDH=∠C,得到△BDG∽△BAC,△BDH∽△BCA.
∴这样的直线可以作出4条.
(1)若该直线与AC相交,
①过点D作DE∥BC,交AC于点E,则∠AED=∠C,

∵∠A=∠A,
∴△ADE∽△ABC.
②过点D作直线DF交AC于点F,使得∠ADF=∠C,
∵∠A=∠A,
∴△AFD∽△ABC.
(2)同理,若该直线与BC相交,也可作①DG∥AC,②∠BDH=∠C,得到△BDG∽△BAC,△BDH∽△BCA.
∴这样的直线可以作出4条.
点评:本题主要考查对相似三角形的判定,平行线分线段成比例定理等知识点的理解和掌握,能根据题意画出图形是解此题的关键.

练习册系列答案
相关题目
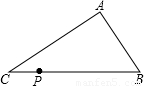
 9、如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( )
9、如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( )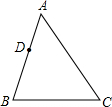 点D是不等边三角形ABC的边AB上的一点,过点D作一条直线,使它与另一边相交截得的三角形与△ABC相似,这样的直线可以作几条?为什么?
点D是不等边三角形ABC的边AB上的一点,过点D作一条直线,使它与另一边相交截得的三角形与△ABC相似,这样的直线可以作几条?为什么?