题目内容
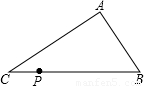
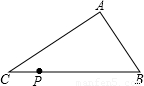
如图，已知点P是不等边△ABC的边BC上的一点，点D在边AB或AC上，若由点P、D截得的小三角形与△ABC相似，那么D点的位置最多有（ ）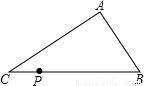
A．2处
B．3处
C．4处
D．5处
【答案】分析：可先判断由点P、D截得的小三角形与△ABC有哪些相等的条件，然后根据相似三角形的判定方法来判断符合条件的D点有几个．
解答：解：①△CPD与△CBA相似；此时△CPD与△CBA共用∠C，P点的位置有两个：
∠CPD=∠B或∠CPD=∠A；
②△BPD与△BCA相似；此时△CPD与△CBA共用∠B，P点的位置同样有两个：
∠BPD=∠C或∠BPD=∠A；
所以符合条件的D点位置最多有4处；
故选C．
点评：此题主要考查的是相似三角形的判定；需注意的是不同的对应角相等，能得出不同的相似三角形，不要漏解．
解答：解：①△CPD与△CBA相似；此时△CPD与△CBA共用∠C，P点的位置有两个：
∠CPD=∠B或∠CPD=∠A；
②△BPD与△BCA相似；此时△CPD与△CBA共用∠B，P点的位置同样有两个：
∠BPD=∠C或∠BPD=∠A；
所以符合条件的D点位置最多有4处；
故选C．
点评：此题主要考查的是相似三角形的判定；需注意的是不同的对应角相等，能得出不同的相似三角形，不要漏解．
练习册系列答案
相关题目
9、如图，已知点P是不等边△ABC的边BC上的一点，点D在边AB或AC上，若由点P、D截得的小三角形与△ABC相似，那么D点的位置最多有（ ）
