题目内容
已知反比例函数y=| k |
| 2x |
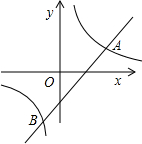 2)两点.
2)两点.(1)求反比例函数的解析式;
(2)求反比例函数与一次函数两个交点A、B的坐标:
(3)根据函数图象,求不等式
| k |
| 2x |
(4)在(2)的条件下,x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
分析:(1)将点(a,b),(a+k,b+k+2)分别代入一次函数解析式,即可得出关于b的等式,即可得出答案;
(2)利用(1)中k的值,得出反比例函数解析式,将两函数组成方程组,求出交点坐标即可;
(3)利用函数图象交点坐标,即可得出不等式
>2x-1的解集;
(4)分别根据当AP1⊥x轴时,当AO=OP2时,当AO=AP3时,当AO=P4O时,得出答案即可.
(2)利用(1)中k的值,得出反比例函数解析式,将两函数组成方程组,求出交点坐标即可;
(3)利用函数图象交点坐标,即可得出不等式
| k |
| 2x |
(4)分别根据当AP1⊥x轴时,当AO=OP2时,当AO=AP3时,当AO=P4O时,得出答案即可.
解答:解:(1)∵一次函数的图象经过(a,b),(a+k,b+k+2)两点,
∴b=2a-1①,2a+2k-1=b+k+2②,
∴整理②得:b=2a-1+k-2,
∴由①②得:2a-1=2a-1+k-2,
∴k-2=0,
∴k=2,
∴反比例函数的解析式为:y=
=
;
(2)解方程组
,
解得:
,
,
∴A(1,1),B(-
,-2);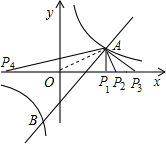
(3)根据函数图象,可得出不等式
>2x-1的解集;
即0<x<1或x<-
;
(4)当AP1⊥x轴,AP1=OP1,∴P1(1,0),
当AO=OP2,∴P2(
,0),
当AO=AP3,∴P3(2,0),
当AO=P4O,∴P4(-
,0).
∴存在P点P1(1,0),P2(
,0),P3(2,0),P4(-
,0).
∴b=2a-1①,2a+2k-1=b+k+2②,
∴整理②得:b=2a-1+k-2,
∴由①②得:2a-1=2a-1+k-2,
∴k-2=0,
∴k=2,
∴反比例函数的解析式为:y=
| 2 |
| 2x |
| 1 |
| x |
(2)解方程组
|
解得:
|
|
∴A(1,1),B(-
| 1 |
| 2 |

(3)根据函数图象,可得出不等式
| k |
| 2x |
即0<x<1或x<-
| 1 |
| 2 |
(4)当AP1⊥x轴,AP1=OP1,∴P1(1,0),
当AO=OP2,∴P2(
| 2 |
当AO=AP3,∴P3(2,0),
当AO=P4O,∴P4(-
| 2 |
∴存在P点P1(1,0),P2(
| 2 |
| 2 |
点评:此题主要考查了一次函数与反比例函数的综合应用,以及交点坐标求法和等腰三角形的性质等知识,根据图象上点的性质得出2a-1=2a-1+k-2,从而得出k的值是解决问题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 面积为3,若直线y=ax+b经过点A,并且经过反比例函数
面积为3,若直线y=ax+b经过点A,并且经过反比例函数 已知反比例函数
已知反比例函数