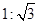题目内容
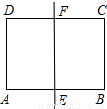
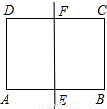
如图,一张矩形报纸ABCD的长AB=acm,宽BC=bcm,E、F分别是AB,CD的中点、将这张报纸沿着直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比.则a:b= .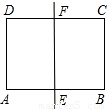
【答案】分析:根据相似形对应角相等,对应边的比相等,即可求解
解答:解:∵ABCD的长AB=acm,宽BC=bcm,E、F分别是AB,CD的中点、
∴矩形AEFD的长与宽分别是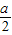 ,b
,b
∴矩形AEFD的长与宽之比等于 ,矩形ABCD的长与宽之比
,矩形ABCD的长与宽之比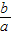 .
.
又∵矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比即于 =
=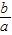 .
.
即b2=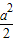 .
.
∴a:b=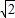 :1.
:1.
故答案为: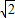 :1.
:1.
点评:本题考查相似多边形的性质.相似多边形对应边成比例.
解答:解:∵ABCD的长AB=acm,宽BC=bcm,E、F分别是AB,CD的中点、
∴矩形AEFD的长与宽分别是
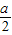 ,b
,b∴矩形AEFD的长与宽之比等于
 ,矩形ABCD的长与宽之比
,矩形ABCD的长与宽之比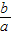 .
.又∵矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比即于
 =
=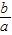 .
.即b2=
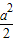 .
.∴a:b=
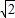 :1.
:1.故答案为:
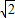 :1.
:1.点评:本题考查相似多边形的性质.相似多边形对应边成比例.

练习册系列答案
相关题目
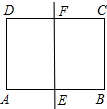 如图,一张矩形报纸ABCD的长AB=acm,宽BC=bcm,E、F分别是AB,CD的中点、将这张报纸沿着直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比.则a:b=
如图,一张矩形报纸ABCD的长AB=acm,宽BC=bcm,E、F分别是AB,CD的中点、将这张报纸沿着直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比.则a:b=
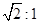 B、
B、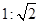 C、
C、 D、
D、