题目内容
?ABCD中,O是对角线的交点,不能判定这个平行四边形是正方形的是
- A.∠BAD=90°,AB=AD
- B.∠BAD=90°,AC⊥BD
- C.AC⊥BD,AC=BD
- D.AB=AC,∠BAD=∠BCD
D
分析:根据正方形的判定:对角线互相垂直平分且相等的四边形是正方形进行分析从而得到最后的答案.
解答:A:根据AB=AD可得出平行四边形是菱形,再利用∠BAD=90°,能判定为正方形,故此选项不符合题意;
B:根据AC⊥BD可得出平行四边形是菱形,再利用∠BAD=90°,能判定为正方形,故此选项不符合题意;
C:根据AC⊥BD可得出平行四边形是菱形,再利用AC=BD,能判定为正方形,故此选项不符合题意;
D:根据AB=AD可得出平行四边形是菱形,∠BAD=∠BCD是所有平行四边形具有的性质,故不能判定是正方形,故此选项符合题意;
故选:D.
点评:本题是考查了正方形的判定,判别一个四边形为正方形主要根据正方形的概念,途经有两种:①先说明它是矩形,再说明有一组邻边相等;②先说明它是菱形,再说明它有一个角为直角.
分析:根据正方形的判定:对角线互相垂直平分且相等的四边形是正方形进行分析从而得到最后的答案.
解答:A:根据AB=AD可得出平行四边形是菱形,再利用∠BAD=90°,能判定为正方形,故此选项不符合题意;
B:根据AC⊥BD可得出平行四边形是菱形,再利用∠BAD=90°,能判定为正方形,故此选项不符合题意;
C:根据AC⊥BD可得出平行四边形是菱形,再利用AC=BD,能判定为正方形,故此选项不符合题意;
D:根据AB=AD可得出平行四边形是菱形,∠BAD=∠BCD是所有平行四边形具有的性质,故不能判定是正方形,故此选项符合题意;
故选:D.
点评:本题是考查了正方形的判定,判别一个四边形为正方形主要根据正方形的概念,途经有两种:①先说明它是矩形,再说明有一组邻边相等;②先说明它是菱形,再说明它有一个角为直角.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 12、如图,在?ABCD中,F是AD延长线上一点,连接BF交DC于点E,则图中的位似三角形共有
12、如图,在?ABCD中,F是AD延长线上一点,连接BF交DC于点E,则图中的位似三角形共有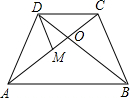 如图,四边形ABCD中,M是AC上一点,若∠ADM=∠BDC,
如图,四边形ABCD中,M是AC上一点,若∠ADM=∠BDC,
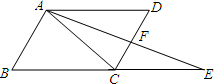 如图,平行四边形ABCD中,E是BC边延长线上一点,AE交CD于F,则图中相似三角形有
如图,平行四边形ABCD中,E是BC边延长线上一点,AE交CD于F,则图中相似三角形有