题目内容
已知在△ABC中,AB=AC=6,且△ABC的面积是12.(1)①在图1中,求BD的长.②在图2中,P是BC的中点,求PM+PN.
(2)图3中,对于BC边上任意一点P,请对点P到两腰距离和(PM+PN)与腰上高(CQ)的大小关系提出猜想,并加以证明.
(3)如图4,在矩形ABCD中,P是CD边任意一点,AD=3,CD=4,请直接写出P到BD、AC的距离和PM+PN.

分析:(1)①根据三角形的面积公式列式即可求解,②连接AP,把△ABC分成两个三角形,△APB与△APC,然后利用△ABC的面积的两种不同表示即可得解;
(2)连接AP,把△ABC分成两个三角形,△APB与△APC,然后利用△ABC的面积=△APB的面积+△APC的面积,又AB=AC,整理即可得解;
(3)连接OP,过点D作DE⊥AC,垂足为E,根据(2)中的结论PM+PN=DE,利用勾股定理求出AC的长度,再利用△ACD的面积求出DE的长度,即可得解.
(2)连接AP,把△ABC分成两个三角形,△APB与△APC,然后利用△ABC的面积=△APB的面积+△APC的面积,又AB=AC,整理即可得解;
(3)连接OP,过点D作DE⊥AC,垂足为E,根据(2)中的结论PM+PN=DE,利用勾股定理求出AC的长度,再利用△ACD的面积求出DE的长度,即可得解.
解答:解:(1)①△ABC的面积=
×AC×BD,
∴
×6×BD=12,
解得BD=4,
②连接AP,则△ABC的面积=△APB的面积+△APC的面积,
即
×AC×BD=
×AB×PM+
×AC×PN,
∵AB=AC,
∴BD=PM+PN,
∴PM+PN=4;
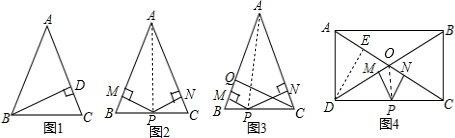
(2)PM+PN=CQ.
理由如下:连接AP,则△ABC被分成△APB与△APC,
∴△ABC的面积=△APB的面积+△APC的面积,
即
×AC×CQ=
×AB×PM+
×AC×PN,
∵AB=AC,
∴PM+PN=CQ;
(3)过D作DE⊥AC,垂足为E,根据(2)的结论得,PM+PN=DE,
∵AD=3,CD=4,
∴AC=
=
=5,
S△ABC=
×AD×CD=
×AC×DE,
即
×3×4=
×5×DE,
解得DE=
,
∴PM+PN=
.
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得BD=4,
②连接AP,则△ABC的面积=△APB的面积+△APC的面积,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴BD=PM+PN,
∴PM+PN=4;

(2)PM+PN=CQ.
理由如下:连接AP,则△ABC被分成△APB与△APC,
∴△ABC的面积=△APB的面积+△APC的面积,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴PM+PN=CQ;
(3)过D作DE⊥AC,垂足为E,根据(2)的结论得,PM+PN=DE,
∵AD=3,CD=4,
∴AC=
| AD2+CD2 |
| 32+42 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得DE=
| 12 |
| 5 |
∴PM+PN=
| 12 |
| 5 |
点评:本题考查了矩形的性质,等腰三角形的性质,利用三角形的面积公式列出算式并整理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数. 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.