题目内容
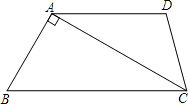
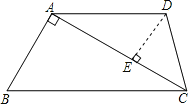
【题目】如图,在梯形ABCD中,AD∥BC,∠B=60°,∠ADC=105°,AD=6,且AC⊥AB,求AB的长.
【答案】![]()
【解析】
由于∠B=60°,AC⊥AB可以得到∠BCA=90°-60°=30°,又由AD∥BC可以推出∠DAC=∠BCA,然后即可得到∠DCE的度数.再根据直角三角形的性质求出AC,最后利用三角函数求出AB长.
过点D作DE⊥AC于点E,则∠AED=∠DEC=90°,
∵ AC⊥AB,
∴ ∠BAC=90°,
∵ ∠B=60°,
∴ ∠ACB=30°,
∵ AD∥BC,
∴ ∠DAC=∠ACB=30°,
∴ 在Rt△ADE中,DE=![]() AD=3,AE=
AD=3,AE=![]() ,∠ADE=60°,
,∠ADE=60°,
∵ ∠ADC=105°,
∴ ∠EDC=45°,
∴ 在Rt△CDE中, CE=DE=3,
∴ AC=AE+CE=![]() ,
,
∴ 在Rt△ABC中,AB=AC![]() tan∠ACB=
tan∠ACB=![]() .
.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目